Visualization with R Lecture (Part 2)
Background
This document contains all the code used to generate the images for lecture number 8 of BGGN-213 (Foundations of Bioinformatics) and follows on from Part 1.. This document is not meant to stand alone – it has very little explanatory text. It is meant to be a reference for students who want to see how the plots for the presentation were made.
Setup
First I set up a theme for presentations. It uses white on black (good for large, dimly lit rooms), and lines and text that are too small/fine when rendered in a document, but which work well when rendered at 300dpi for the presnetation. Note that I would usually not use white on black for documents, but I use this as the default theme throughout because there isn’t an easy way (that I know of) to set the default color of a geom to something other than black.
theme_preso <- theme_dark(base_size=11)
##theme_set(theme_preso)
preso_save<-function(filename, plot=last_plot(), theme=theme_preso,
width=1280/300, height=720/300, dpi=300) {
ggsave(filename, ##plot+theme,
width=width, height=height, dpi=dpi)
}
Part 1: Why visualize at all?
A circle
Showing the data in a scatterplot makes the relationship obivous pre-attentively.
circle<-read.delim(textConnection(
"x y
1.972 1.236
1.112 1.994
0 1.009
0.665 1.942
0.235 0.356
0.247 1.658
1.275 1.961
0.702 0.045
1.76 0.35
1.691 0.277
1.628 1.778
1.957 1.29
0.111 0.542
0.902 0.005
0.598 0.085
1.613 1.79
1.298 1.955
0.651 1.937
1.949 1.316
0.099 0.567
0.862 0.01
0.027 0.768
0.706 1.956
1.042 1.999"))
ggplot(circle, aes(x,y))+geom_point(color="black", size=2)+coord_equal()
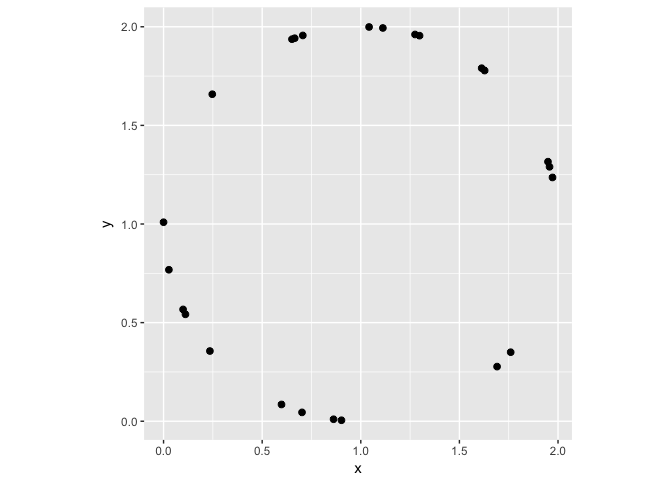
preso_save("img/circle.png")
But showing it as a time-series obscures the relationship. This is arguably worse than a simple table.
circle_w <- circle %>%
mutate(n=1:nrow(circle)) %>%
gather(var, value, x, y)
ggplot(circle_w, aes(n, value, color=var))+geom_line()+xlab(NULL)
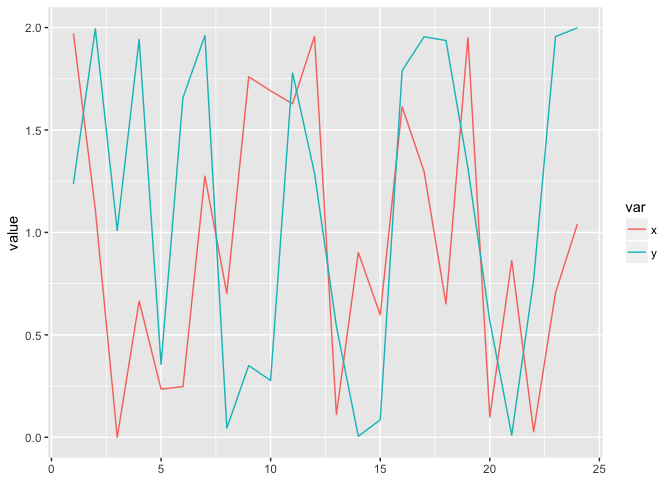
preso_save("img/circle_lines.png")
Anscombe’s Quartet
quartet<-read.delim(textConnection(
"group x y
A 10 8
A 8 7
A 13 7.6
A 9 8.8
A 11 8.3
A 14 10
A 6 7.2
A 4 4.3
A 12 10.8
A 7 4.8
A 5 5.7
B 10 9.1
B 8 8.1
B 13 8.7
B 9 8.8
B 11 9.3
B 14 8.1
B 6 6.1
B 4 3.1
B 12 9.1
B 7 7.3
B 5 4.7
C 10 7.5
C 8 6.8
C 13 12.7
C 9 7.1
C 11 7.8
C 14 8.8
C 6 6.1
C 4 5.4
C 12 8.2
C 7 6.4
C 5 5.7
D 8 6.6
D 8 5.8
D 8 7.7
D 8 8.8
D 8 8.5
D 8 7
D 8 5.3
D 19 12.5
D 8 5.6
D 8 7.9
D 8 6.9"))
All four are identical on common statistical measures.
quartet %>%
group_by(group) %>%
summarize(mean_x=mean(x), mean_y=mean(y))
## # A tibble: 4 x 3
## group mean_x mean_y
## <fctr> <dbl> <dbl>
## 1 A 9 7.500000
## 2 B 9 7.490909
## 3 C 9 7.500000
## 4 D 9 7.509091
quartet %>%
group_by(group) %>%
do(tidy(lm(y~x, data=.))) %>%
select(group, term, estimate) %>%
spread(term, estimate)
## # A tibble: 4 x 3
## # Groups: group [4]
## group `(Intercept)` x
## * <fctr> <dbl> <dbl>
## 1 A 3.008182 0.4990909
## 2 B 2.990909 0.5000000
## 3 C 3.016364 0.4981818
## 4 D 3.017273 0.4990909
quartet %>%
group_by(group) %>%
do(glance(lm(y~x, data=.))) %>%
select(group, r.squared)
## # A tibble: 4 x 2
## # Groups: group [4]
## group r.squared
## <fctr> <dbl>
## 1 A 0.6709131
## 2 B 0.6641054
## 3 C 0.6694547
## 4 D 0.6740641
But obivously different visually.
ggplot(quartet, aes(x,y))+geom_point(color="black")+facet_wrap(~group)
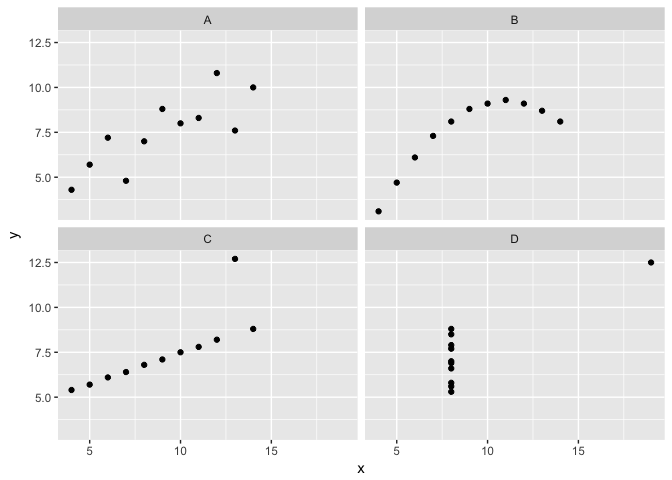
preso_save("img/anscombe.png")
Part 2: Estimation
The hierarchy
The first rule of color is do not talk about color
Color has three separate channels.
values<-data.frame(val=1:5, y=1)
theme_extras <- theme(axis.title=element_blank(),
axis.text=element_blank(),
axis.ticks=element_blank(),
legend.position="none")
ggplot(values, aes(val,y,fill=val)) + geom_tile() + scale_fill_gradient(low="black", high="white", limits=c(0,6)) + theme_extras

preso_save("img/luminance.png", height=720/300/3, theme=theme_preso + theme_extras)
ggplot(values, aes(val,y,fill=val)) + geom_tile() + scale_fill_gradient(low="white", high="red", limits=c(0,6)) + theme_extras
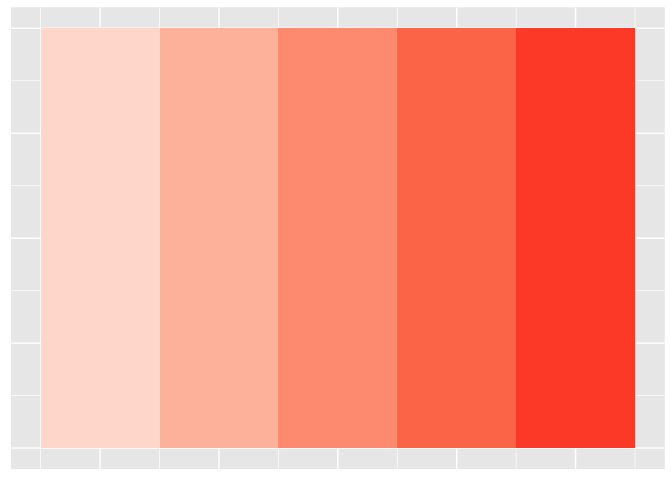
preso_save("img/saturation.png", height=720/300/3, theme=theme_preso + theme_extras)
ggplot(values, aes(val,y,fill=factor(val))) + geom_tile() + scale_fill_discrete() + theme_extras

preso_save("img/hue.png", height=720/300/3, theme=theme_preso + theme_extras)
Lots of plots with the mtcars dataset. I had to drop the font size way down to get the plots the render well for the presentation. They are much too small for the document. I offer my apologies.
# Make model an actual column in the dataset.
mtcars <- mtcars %>%
mutate(model=rownames(mtcars))
Hue
The viridis hue scale. I didn’t end up using this in the presentation. I probably should have, as it’s far superior to the crappy one I made up.
ggplot(mtcars, aes("a", model, fill=mpg))+geom_tile()+scale_fill_viridis()
ggplot(mtcars, aes("a", reorder(model, mpg), fill=mpg))+geom_tile()+scale_fill_viridis()
Ordered and unordered plots with hue encoding efficiency.
theme_extras <- theme(axis.title.x=element_blank(),
axis.text.x=element_blank(),
axis.ticks.x=element_blank(),
axis.text.y=element_text(size=rel(0.6)))
ggplot(mtcars, aes("a", model, fill=mpg)) +
geom_tile() +
scale_fill_gradient2(midpoint=median(mtcars$mpg), mid="#ffffbf", low="#91bfdb", high="#fc8d59") +
# Terrible for color blind people
# scale_fill_gradient2(midpoint=median(mtcars$mpg), mid=muted("green")) +
ylab(NULL) + theme_extras
preso_save("img/mtcars_hue.png", width=1280/300*(3/4), theme=theme_preso+theme_extras)
ggplot(mtcars, aes("a", reorder(model, mpg), fill=mpg)) +
geom_tile() +
scale_fill_gradient2(midpoint=median(mtcars$mpg), mid="#ffffbf", low="#91bfdb", high="#fc8d59") +
# Terrible for color blind people
# scale_fill_gradient2(midpoint=median(mtcars$mpg), mid=muted("green")) +
ylab(NULL) + theme_extras

preso_save("img/mtcars_hue_ordered.png", width=1280/300*(3/4), theme=theme_preso+theme_extras)
Saturation
Unordered and ordered plots with saturation.
ggplot(mtcars, aes("a", model, fill=mpg)) +
geom_tile() +
scale_fill_gradient(low="white", high=muted("blue"))+
ylab(NULL) + theme_extras

preso_save("img/mtcars_saturation.png", width=1280/300*(3/4), theme=theme_preso+theme_extras)
ggplot(mtcars, aes("a", reorder(model, mpg), fill=mpg)) +
geom_tile() +
scale_fill_gradient(low="white", high=muted("blue"))+
ylab(NULL) + theme_extras

preso_save("img/mtcars_saturation_ordered.png", width=1280/300*(3/4), theme=theme_preso+theme_extras)
For accurate ratioing with saturation, the scale has to extend to zero.
ggplot(mtcars, aes("a", reorder(model, mpg), fill=mpg)) +
geom_tile() +
scale_fill_gradient(low="white", high=muted("blue"))+
ylab(NULL) + theme_extras + expand_limits(fill=0)

preso_save("img/mtcars_saturation_expanded.png", width=1280/300*(3/4), theme=theme_preso+theme_extras)
Area
mtcars <- mtcars %>%
mutate(model=reorder(model, mpg)) %>%
arrange(mpg, model)
theme_extras <- theme(axis.title=element_blank(),
axis.text=element_blank(),
axis.ticks=element_blank())
cols<-4
ggplot(mtcars, aes(rep(1:cols, 32/cols), rep(1:(32/cols), each=cols))) +
geom_point(aes(size=mpg), color="black") +
geom_text(aes(label=model), color="black", position=position_nudge(y=0.5), size=2) +
expand_limits(x=c(0.5,4.5), y=c(1,8.5))+ ylab(NULL) + scale_size_area() + theme_extras

preso_save("img/mtcars_area.png", theme=theme_preso+theme_extras)
Again, accurate ratioing depends on a scale that goes to zero.
ggplot(mtcars, aes(rep(1:cols, 32/cols), rep(1:(32/cols), each=cols))) +
geom_point(aes(size=mpg), color="black") +
geom_text(aes(label=model), color="black", position=position_nudge(y=0.5), size=2) +
expand_limits(x=c(0.5,4.5), y=c(1,8.5), size=15)+ ylab(NULL) + theme_extras

preso_save("img/mtcars_area_nonzero.png", theme=theme_preso+theme_extras)
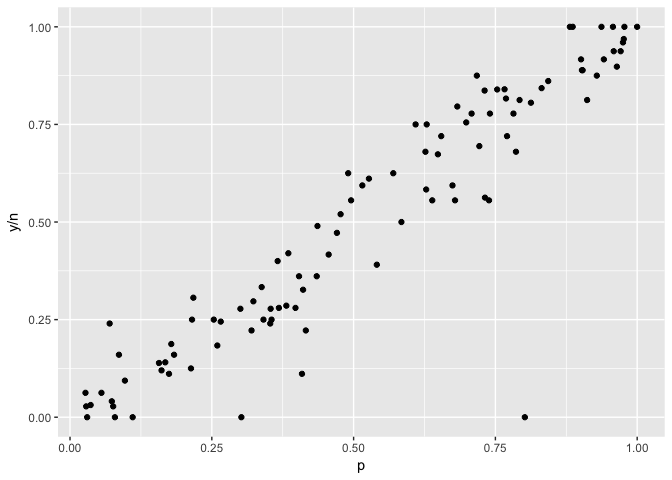
“Bubble charts” use size to indicate the weight of a point. In these plots the outliers have low weight (small size).
to_plot<-data.frame(p=runif(100),
n=rpois(100, 5)^2) %>%
mutate(y=rbinom(100,n,p))
ggplot(to_plot,aes(p,y/n,size=n)) +geom_point(color="black") +scale_size_area()
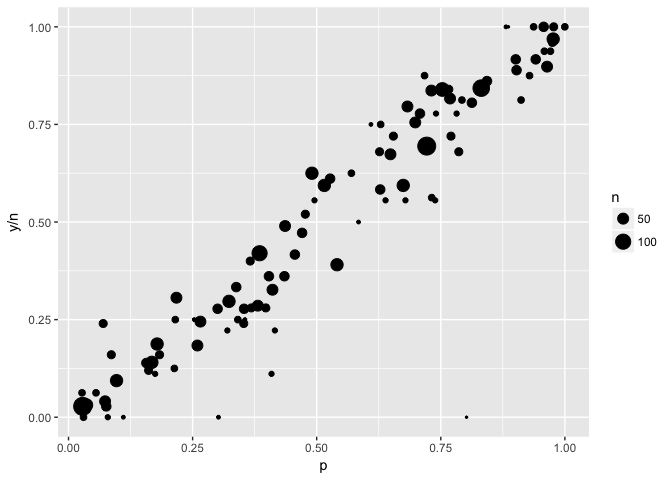
ggplot(to_plot,aes(p,y/n)) +geom_point(color="black")
to_plot<-data.frame(trial=1:100,
n=rpois(100, 5)^2) %>%
mutate(y=rbinom(100,n,0.5)/n)
ggplot(to_plot, aes(trial, y)) + geom_point(color="black")
## Warning: Removed 1 rows containing missing values (geom_point).
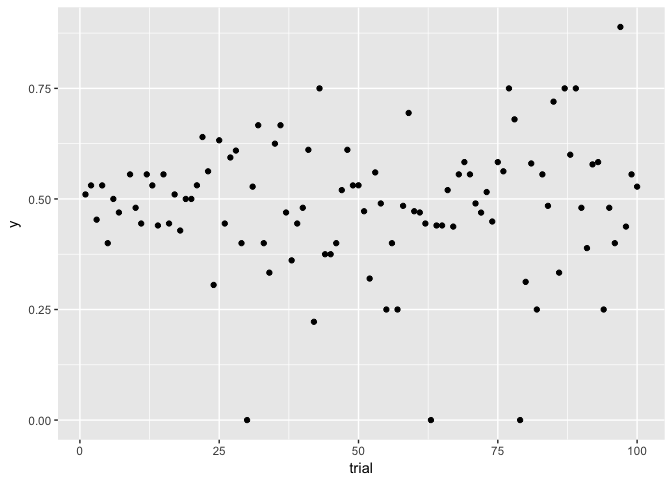
preso_save("img/flips_same.png")
## Warning: Removed 1 rows containing missing values (geom_point).
ggplot(to_plot, aes(trial, y, size=n)) + geom_point(color="black", alpha=2/3) + scale_size_area()
## Warning: Removed 1 rows containing missing values (geom_point).
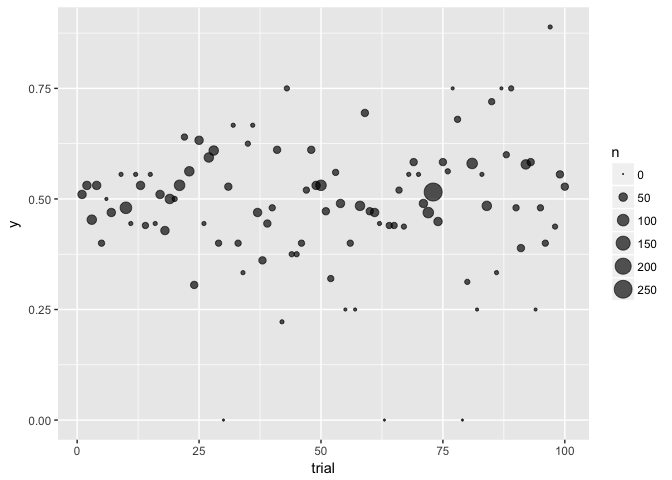
preso_save("img/flips_area.png")
## Warning: Removed 1 rows containing missing values (geom_point).
Angle
Again, note that the scale goes to zero (a horizontal line).
make_segment <- function(df, scale_low, scale_high) {
scale_range <- scale_high-scale_low
fraction <- (df$mpg-scale_low) / scale_range
theta <- fraction * pi/2
return(data.frame(x=c(0, cos(theta)),
y=c(0, sin(theta))))
}
mtcars_angle <- mtcars %>%
group_by(model) %>%
do(make_segment(., 0, max(mtcars$mpg)))
# do(make_segment(., min(mtcars$mpg), max(mtcars$mpg)))
theme_extras <- theme(axis.title=element_blank(),
axis.text=element_blank(),
axis.ticks=element_blank(),
strip.text.x = element_text(size=rel(0.5), hjust=0))
ggplot(mtcars_angle, aes(x,y,group=model))+
geom_path(color="black")+
facet_wrap(~model,ncol=8)+coord_equal() +
theme_extras

preso_save("img/mtcars_slope.png", theme=theme_preso+theme_extras)
Length
In the presentation, I use the jittered bars, so that the audience can’t rely on a common scale (which is next in the hierarchy).
theme_extras <- theme(axis.text.y=element_text(size=rel(0.7)),
axis.title.x=element_blank(),
axis.text.x=element_blank(),
axis.ticks.x=element_blank())
mtcars$random <- runif(32,0,5)
ggplot(mtcars, aes(x=random, xend=mpg+random, y=model, yend=model)) +
geom_segment(size=2, color="black") + xlab(NULL) + ylab(NULL) + theme_extras

preso_save("img/mtcars_length.png", theme=theme_preso+theme_extras)
theme_extras <- theme(axis.text.y=element_text(size=rel(0.7)))
ggplot(mtcars, aes(x=0, xend=mpg, y=model, yend=model)) +
geom_segment(size=2, color="black") + xlab(NULL) + ylab(NULL) + theme_extras
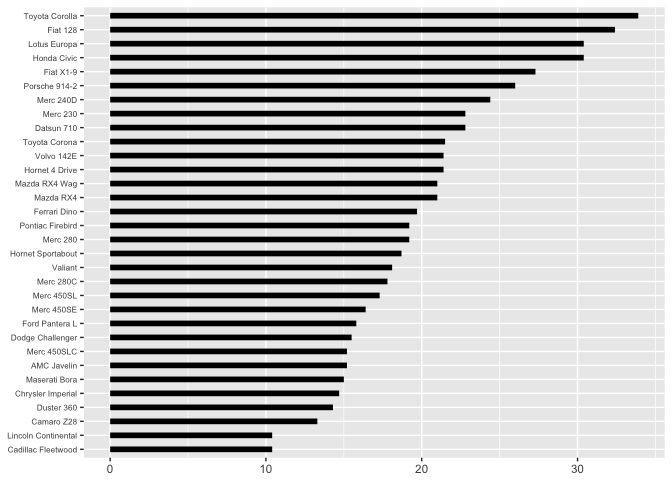
preso_save("img/mtcars_bars.png", theme=theme_preso+theme_extras)
Error bars encode information using length not on a common scale.
trials<-10
flips<-data.frame(trial=1:trials) %>%
mutate(n=round(runif(trials, 20, 500)),
y=rbinom(trials, n, 0.5),
p=y/n,
se=sqrt(p*(1-p)/n),
lower=p-1.96*se,
upper=p+1.96*se)
ggplot(flips, aes(trial, p, ymin=lower, ymax=upper)) + geom_pointrange(color="black")
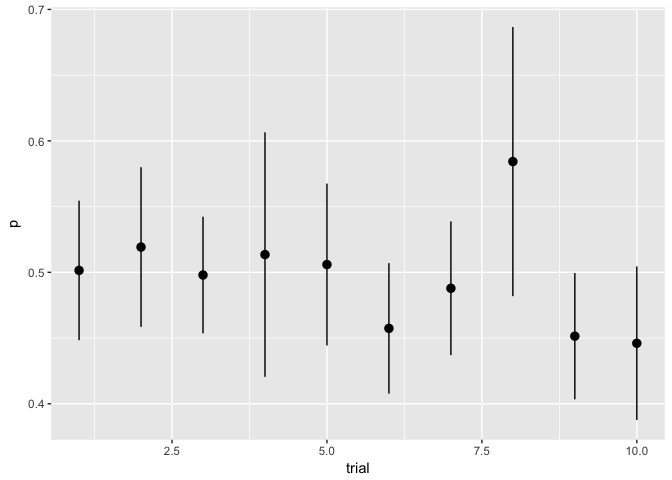
preso_save("img/flips.png")
Position on non-aligned scales
Doing this with facets is the easiest way in ggplot, but uses too much space.
theme_extras <- theme(axis.title.y=element_blank(),
axis.text.y=element_blank(),
axis.ticks.y=element_blank(),
strip.text.x = element_text(size=rel(0.5), hjust=0),
panel.grid.major = element_line(colour = "grey50", size = 0.2),
panel.grid.minor = element_line(colour = "grey50", size = 0.2, linetype="dotted")
)
ggplot(mtcars, aes(x=mpg, y="a")) + geom_point(color="black", size=1) +
scale_x_continuous(breaks=c(10,20,30)) +
facet_wrap(~model, ncol=8) + theme_extras
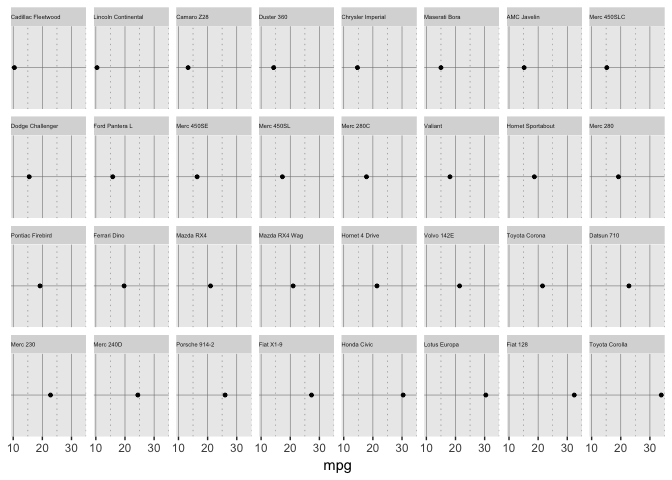
preso_save("img/mtcars_nonaligned.png", theme=theme_preso+theme_extras)
Position on a common scale
Ahhhh…
theme_extras <- theme(axis.text.y=element_text(size=rel(0.7)),
axis.title.y=element_text(size=rel(0.7)),
panel.grid.major = element_line(colour = "grey20", size = 0.2))
ggplot(mtcars, aes(x=mpg, y=model)) +
geom_point(color="black") +
theme_extras + ylab(NULL)
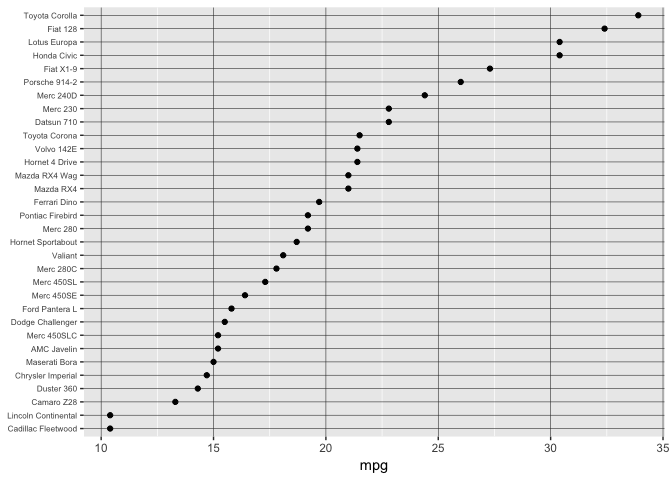
preso_save("img/mtcars_aligned.png", theme=theme_preso+theme_extras)
Ordering still crucial.
mtcars$model2<-factor(as.character(mtcars$model))
ggplot(mtcars, aes(x=mpg, y=model2)) +
geom_point(color="black") +
theme_extras + ylab(NULL)
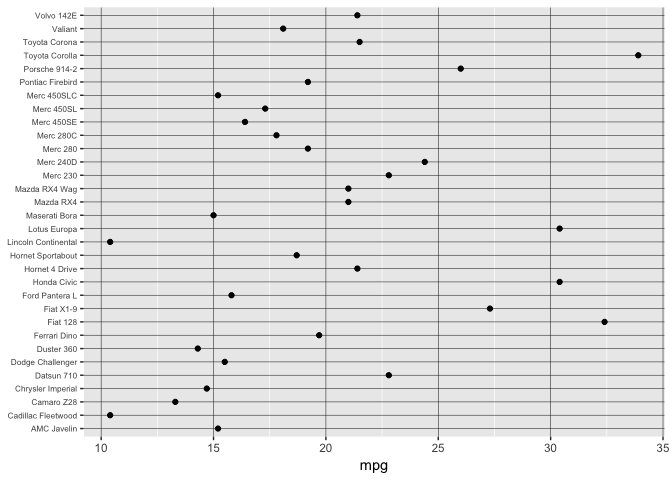
preso_save("img/mtcars_aligned_alpha.png", theme=theme_preso+theme_extras)
Dropping the scale to zero is a mistake here, lowers resolution and isn’t needed for accurate ratioing.
ggplot(mtcars, aes(x=mpg, y=model)) +
geom_point(color="black") +
theme_extras + ylab(NULL) + expand_limits(x=0)
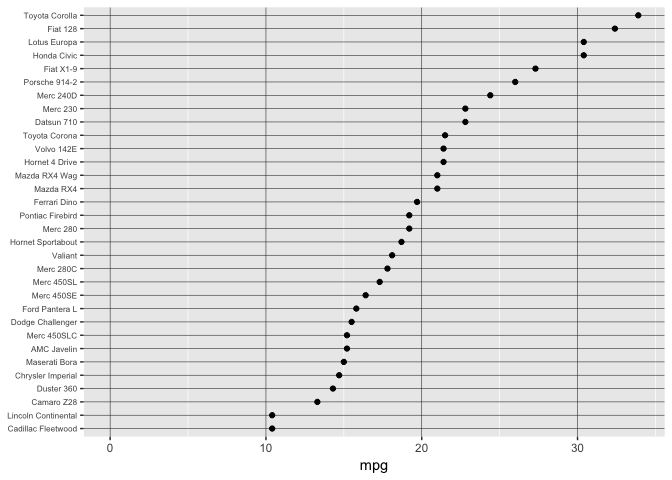
preso_save("img/mtcars_aligned_zero.png", theme=theme_preso+theme_extras)
Observations
Stacked anything is nearly always a mistake
A stacked bar chart does two things, neither of the well.
ggplot(diamonds, aes(clarity, fill=cut, group=cut)) +
geom_bar(stat="count", position="stack") +
scale_y_continuous("Count", labels=comma)
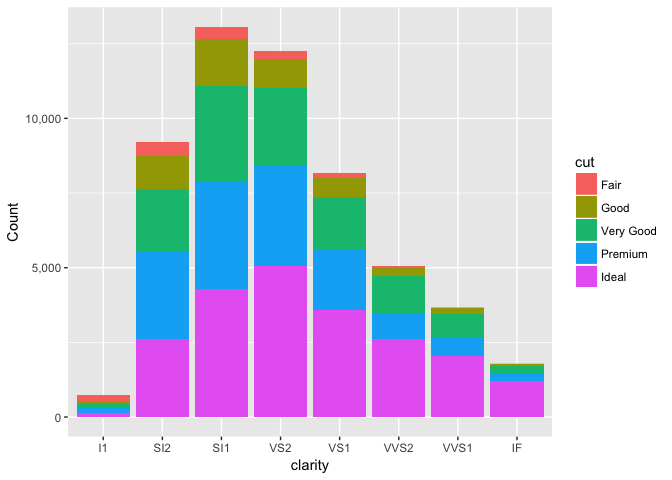
preso_save("img/diamonds_stack.png")
The first is the total in each group.
diamonds_summary<-diamonds %>%
group_by(clarity) %>%
summarize(n=length(clarity))
ggplot(diamonds_summary, aes(clarity, n)) +
geom_line(group=1, color="black") +
geom_point(color="black") +
expand_limits(y=0) +
scale_y_continuous("Count", labels=comma)
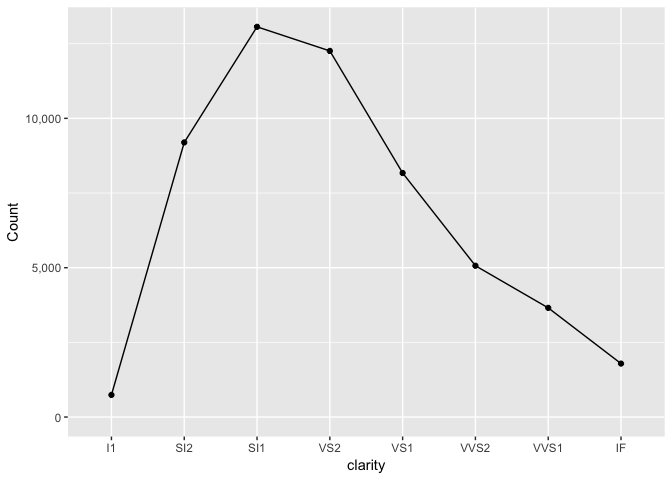
preso_save("img/diamonds_overall.png")
The second in the total in each combination, which is better shown with a parallel coordinates plot.
diamonds_summary2<-diamonds %>%
group_by(clarity, cut) %>%
summarize(n=length(clarity))
ggplot(diamonds_summary2, aes(clarity, n, color=cut, group=cut)) +
geom_line() +
geom_point() +
expand_limits(y=0) +
scale_y_continuous("Count", labels=comma)
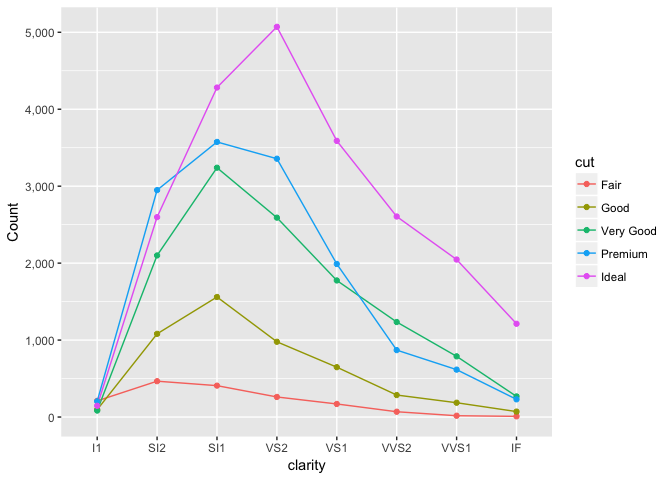
preso_save("img/diamonds_freqpoly.png")
Some phone data (from wikipedia).
phone_data<-
"Quarter Windows Mobile RIM Symbian iOS Android Bada Windows Phone Other
2016 Q2[39] 0 400.4 0 44395 296912 0 1971 680.6
2016 Q1[40] 0 660 0 51630 293771 0 2400 791
2015 Q4[41] 0 906.9 0 71526 325394 0 4395 887.3
2015 Q3[42] 0 977 0 46062 298797 0 5874 1133.6
2015 Q2[43] 0 1153 0 48086 271010 0 8198 1229
2015 Q1[44] 0 1325 0 60177 265012 0 8271 1268
2014 Q4[45] 0 1734 0 74832 279058 0 10425 1286.9
2014 Q3[46] 0 2420 0 38187 254354 0 9033 1310.2
2014 Q2[47] 0 2044 0 35345 243484 0 8095 2044
2014 Q1[44] 0 1714 0 43062 227549 0 7580 1371
2013 Q4[48] 0 1807 0 50224 219613 0 8534 1994
2013 Q3[49] 0 4401 458 30330 205023 633 8912 475
2013 Q2[50] 0 6180 631 31900 177898 838 7408 472
2013 Q1[51] 0 6219 1349 38332 156186 1371 5989 600
2012 Q4[52] 0 7333 2569 43457 144720 2684 6186 713
2012 Q3[53] 0 8947 4405 23550 122480 5055 4058 684
2012 Q2[54] 0 7991 9072 28935 98529 4209 4087 863
2012 Q1[55] 0 9939 12467 33121 81067 3842 2713 1243
2011 Q4[56] 0 13185 17458 35456 75906 3111 2759 1167
2011 Q3[57] 0 12701 19500 17295 60490 2479 1702 1018
2011 Q2[58] 0 12652 23853 19629 46776 2056 1724 1051
2011 Q1 982 13004 27599 16883 36350 1862 1600 1495
2010 Q4[56] 3419 14762 32642 16011 30801 2027 0 1488
2010 Q3[57] 2204 12508 29480 13484 20544 921 0 1991
2010 Q2[58] 3059 11629 25387 8743 10653 577 0 2011
2010 Q1[59] 3696 10753 24068 8360 5227 0 0 2403
2009 Q4[60] 4203 10508 23857 8676 4043 0 0 2517
2009 Q3[61] 3260 8523 18315 7040 1425 0 0 2531
2009 Q2[62] 3830 7782 20881 5325 756 0 0 2398
2009 Q1[63] 3739 7534 17825 3848 575 0 0 2986
2008 Q4[64] 4714 7443 17949 4079 639 0 0 3319
2008 Q3[65] 4053 5800 18179 4720 0 0 0 3763
2008 Q2[66] 3874 5594 18405 893 0 0 0 3456
2008 Q1[64] 3858 4312 18400 1726 0 0 0 4113
2007 Q4[64] 4374 4025 22903 1928 0 0 0 3536
2007 Q3[65] 4180 3192 20664 1104 0 0 0 3612
2007 Q2[66] 3212 2471 18273 270 0 0 0 3628
2007 Q1[64] 2931 2080 15844 0 0 0 0 4087"
phones<-read.delim(textConnection(phone_data))
phones <- phones %>%
mutate(Other = Other + Bada + Windows.Phone,
Bada = NULL,
Windows.Phone = NULL,
Quarter = str_replace(Quarter, "\\[\\d+\\]", ""),
Year = as.integer(str_split_fixed(Quarter, " ", 2)[,1]),
Quarter = str_split_fixed(Quarter, " ", 2)[,2],
qtr = as.integer(str_replace(Quarter, "Q", "")),
year = Year+0.25*(qtr-1)) %>%
gather(os, ct, -Year, -Quarter, -qtr, -year) %>%
mutate(ct = as.numeric(ct)) %>%
group_by(year) %>%
mutate(share = ct/sum(ct))
phones
## # A tibble: 228 x 7
## # Groups: year [38]
## Quarter Year qtr year os ct share
## <chr> <int> <int> <dbl> <chr> <dbl> <dbl>
## 1 Q2 2016 2 2016.25 Windows.Mobile 0 0
## 2 Q1 2016 1 2016.00 Windows.Mobile 0 0
## 3 Q4 2015 4 2015.75 Windows.Mobile 0 0
## 4 Q3 2015 3 2015.50 Windows.Mobile 0 0
## 5 Q2 2015 2 2015.25 Windows.Mobile 0 0
## 6 Q1 2015 1 2015.00 Windows.Mobile 0 0
## 7 Q4 2014 4 2014.75 Windows.Mobile 0 0
## 8 Q3 2014 3 2014.50 Windows.Mobile 0 0
## 9 Q2 2014 2 2014.25 Windows.Mobile 0 0
## 10 Q1 2014 1 2014.00 Windows.Mobile 0 0
## # ... with 218 more rows
All rules have exceptions. A stacked area chart with phone data is ok because it makes the point more effectively.
ggplot(phones, aes(year, share, group=os, fill=os)) + geom_area()
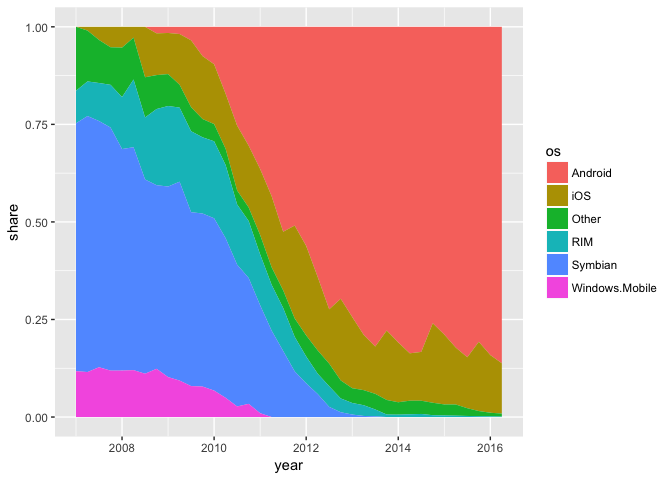
preso_save("img/phones_area.png")
The line chart is weaker.
ggplot(phones, aes(year, share, group=os, color=os)) + geom_line()
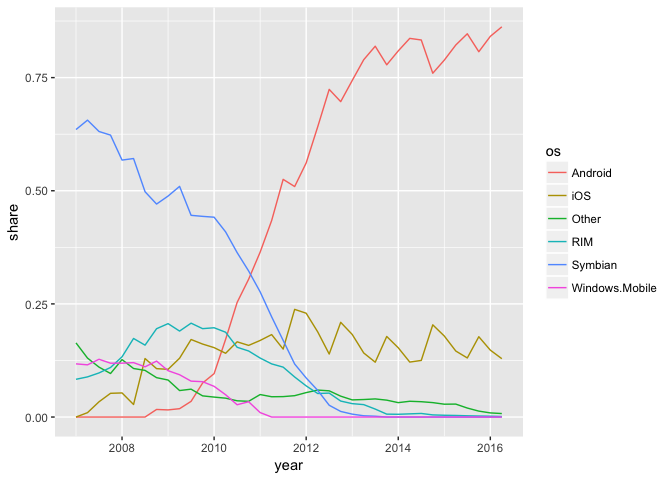
Growth charts usually aren’t
This stacked area chart sucks.
library(gapminder)
continent_pop <- gapminder %>%
group_by(continent, year) %>%
summarize(pop=sum(as.numeric(pop))) %>%
ungroup()
ggplot(continent_pop, aes(year, pop/1e9, group=continent, fill=continent)) +
geom_area() +
scale_y_continuous("Population (Billions)", labels=comma) +
scale_color_brewer(type="qual", palette=1) + xlab(NULL)
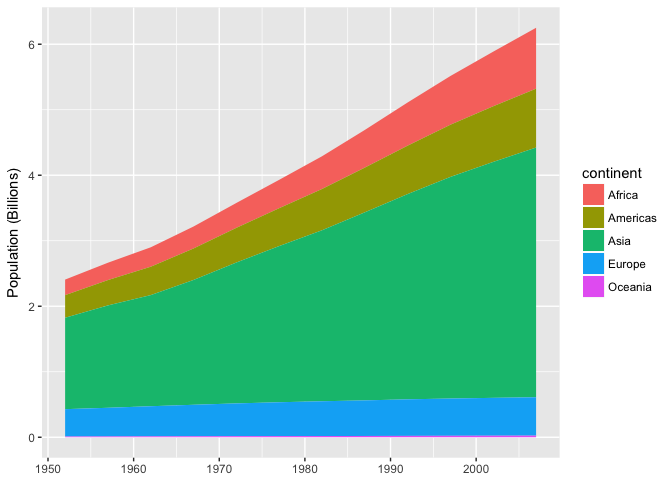
preso_save("img/population_area.png")
This line chart isn’t much better if you care about growth rates, becuse growth is encoded with angle (slope).
ggplot(continent_pop, aes(year, pop/1e9, group=continent, color=continent)) +
geom_line() + scale_y_log10("Population (Billions)", labels=comma) +
scale_color_brewer(type="qual", palette=1) + xlab(NULL)
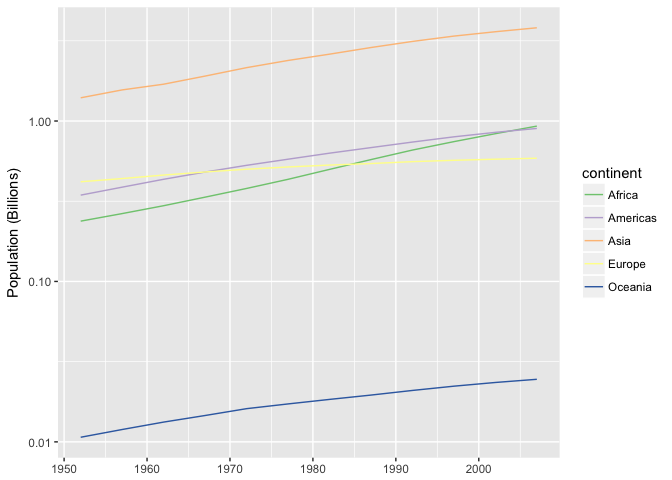
preso_save("img/population.png")
If growth is important, take derivatives and plot growth directly on the y-axis.
continent_pop <- continent_pop %>%
group_by(continent) %>%
arrange(year) %>%
mutate(growth=c(NA,diff(pop)))
ggplot(continent_pop, aes(year, growth/pop, group=continent, color=continent)) +
geom_line() + scale_color_brewer(type="qual", palette=1) +
xlab(NULL) + scale_y_continuous("Pct. Growth", labels=percent)
## Warning: Removed 5 rows containing missing values (geom_path).
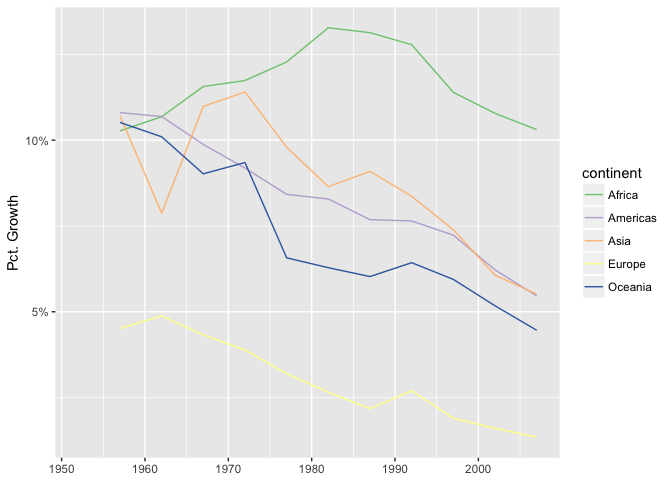
preso_save("img/population_growth.png")
## Warning: Removed 5 rows containing missing values (geom_path).
Putting the data on a common scale helps tremendously
host_dat = data.frame(t=seq.POSIXt(as.POSIXct("2016-06-01 00:00:00"),
as.POSIXct("2016-06-01 01:00:00"),
by=30)) %>%
mutate(cpu=rnorm(length(t), 40, 5),
latency=rnorm(length(t), 4, 0.1))
host_dat$cpu[50] = 100
host_dat$latency[60] = host_dat$latency[60]*3
host_dat_w <- host_dat %>%
gather(var, value, -t) %>%
group_by(var) %>%
mutate(std_value = (value-mean(value))/sd(value))
The user has to work to see if the peaks are aligned.
ggplot(host_dat_w, aes(t, value)) + geom_line(color="black") +
facet_wrap(~var, scales="free") + xlab(NULL)
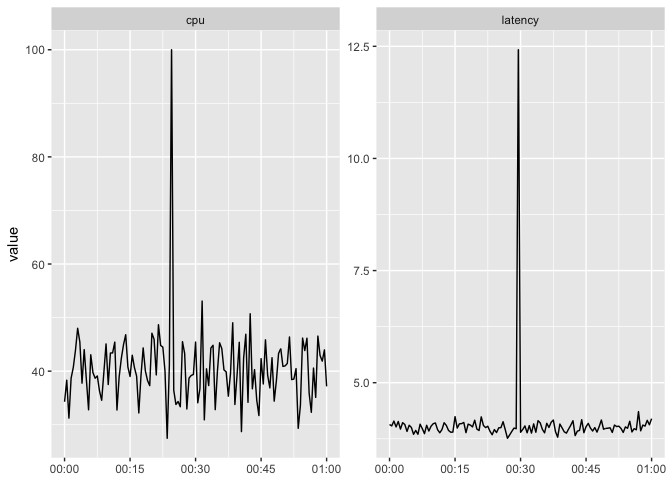
preso_save("img/cpu_latency_nonaligned.png")
You want to put them on the same scale, but the magnitude of the series is different.
ggplot(host_dat_w, aes(t, value, color=var, group=var)) +
geom_line() + xlab(NULL) + ylab("Value")
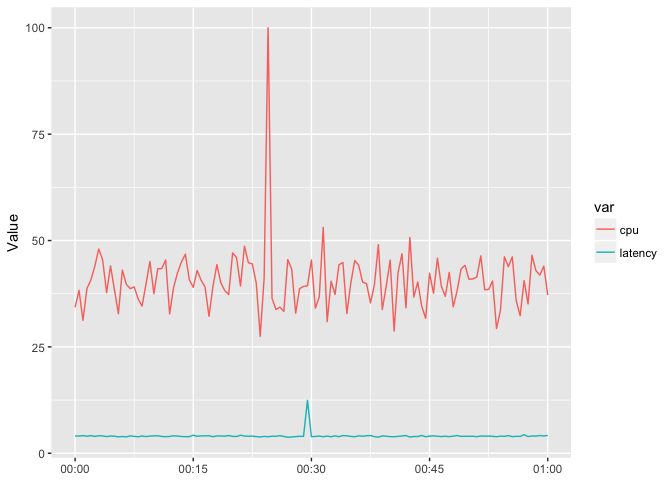
preso_save("img/cpu_latency_aligned.png")
So “standardize” them by suntracting the mean and dividing by the standard deviation.
ggplot(host_dat_w, aes(t, std_value, color=var, group=var)) +
geom_line() + xlab(NULL) + ylab("Standardized Value")
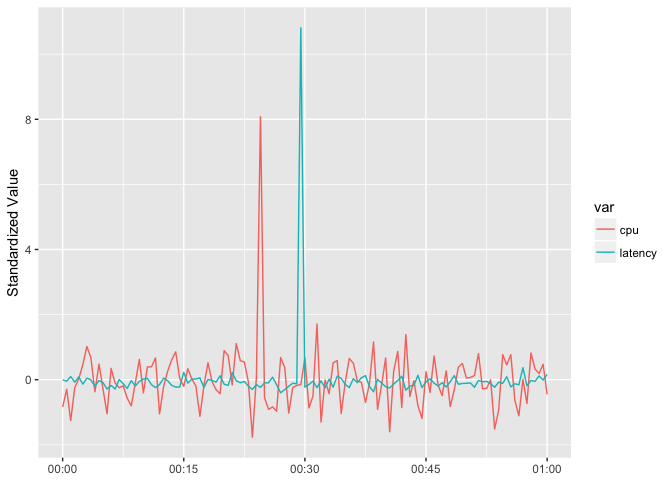
preso_save("img/cpu_latency_std_aligned.png")
TODO: Show deseasonalizing too (usually easy and automatic if many seasonal cycles are available).
Scatter plots show relationships directly
dat <- data.frame(x=seq(1,6*pi,length.out = 100))
# Two series, noe of which varies with the square, the other linearly
dat <- dat %>%
mutate(Dependency=1.4+sin(x),
Service=(1.1+sin(x))^2)
# Jitter the points
dat <- dat %>%
mutate(Service=rnorm(length(x), mean = Service, sd=Service/10),
Dependency=rnorm(length(x), mean = Dependency, sd=Dependency^(2/3)/10))
# Put in long format
dat_l <- dat %>%
gather(var, value, -x)
They move together, but what, preciscely is the nature of the relationship?
ggplot(dat_l, aes(x, value))+geom_line(color="black")+facet_wrap(~var, scales="free")
preso_save("img/ts_vs_scatter_facet.png")
ggplot(dat_l, aes(x, value, color=var))+geom_line()
preso_save("img/ts_vs_scatter_ts.png")
A scatterplot is more revealing.
ggplot(dat, aes(Dependency, Service)) + geom_point(color="black") +
ylab("Some service's latency") + xlab("Its dependency")
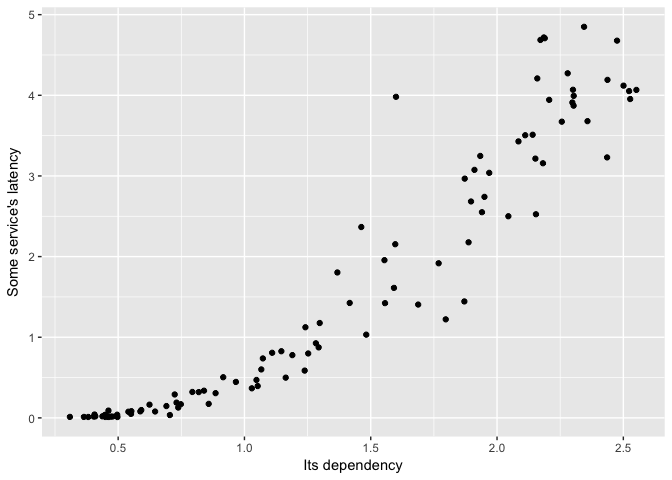
preso_save("img/ts_vs_scatter_scatter.png")
It’s clear that the relationship isn’t linear.
ggplot(dat, aes(Dependency, Service))+geom_point(color="black")+geom_smooth(method="lm") +
ylab("Some service's latency") + xlab("Its dependency")
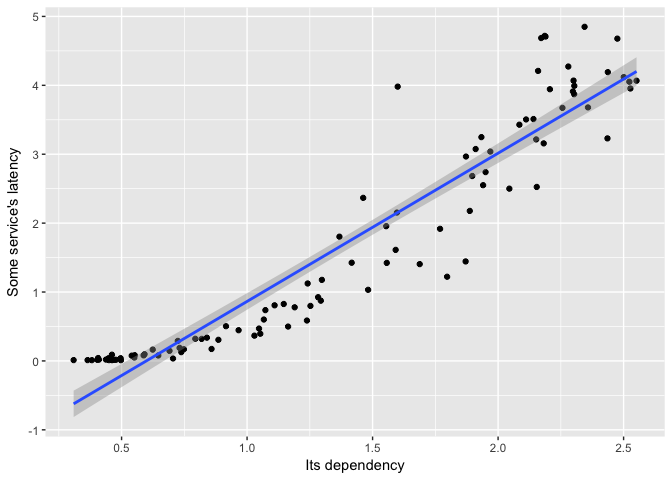
preso_save("img/ts_vs_scatter_lm.png")
A loess fit looks nice.
ggplot(dat, aes(Dependency, Service))+geom_point(color="black")+geom_smooth(method="loess") +
ylab("Some service's latency") + xlab("Its dependency")
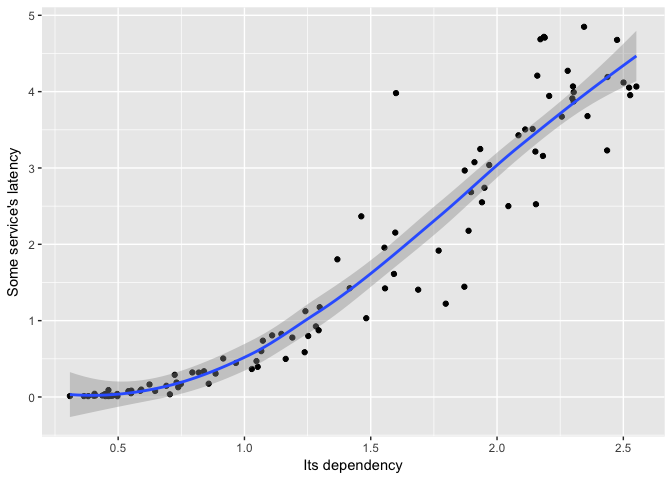
preso_save("img/ts_vs_scatter_loess.png")
Part 3: Assembly
The Law of Continuity
The circle from the start is a good example, as is a simple scatterplot. Note that the continuity just has to be suggestive, not perfect.
ggplot(mtcars, aes(wt, mpg)) +
geom_point(color="black") +
xlab("weight (1,000 lbs)")
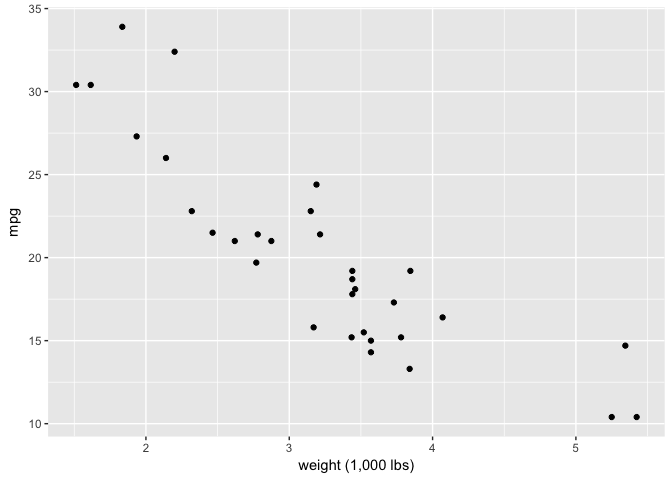
preso_save("img/wt_mpg_scatter.png")
The Law of Similarity
Color is pretty good.
# Make number of cylinders a factor, so ggplot will choose a discrete scale.
mtcars$cyl<-factor(mtcars$cyl)
ggplot(mtcars, aes(wt, mpg)) +
geom_point(aes(color=cyl)) +
xlab("weight (1,000 lbs)") +
scale_color_brewer("Cylinders", type="qual", palette=1)
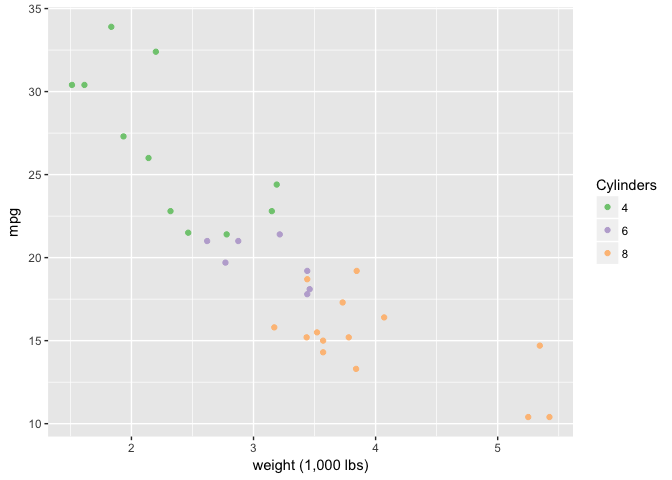
preso_save("img/wt_mpg_scatter_color.png")
These filled shapes aren’t great.
ggplot(mtcars, aes(wt, mpg)) +
geom_point(aes(shape=cyl), color="black") +
xlab("weight (1,000 lbs)") +
scale_shape("Cylinders")
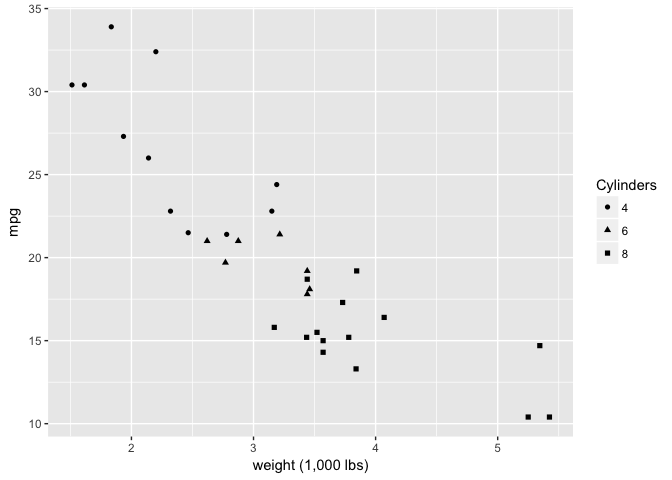
preso_save("img/wt_mpg_scatter_shape1.png")
But these open ones are great.
ggplot(mtcars, aes(wt, mpg)) +
geom_point(aes(shape=cyl), color="black") +
xlab("weight (1,000 lbs)") +
scale_shape_manual("Cylinders", values = c(1,2,3))
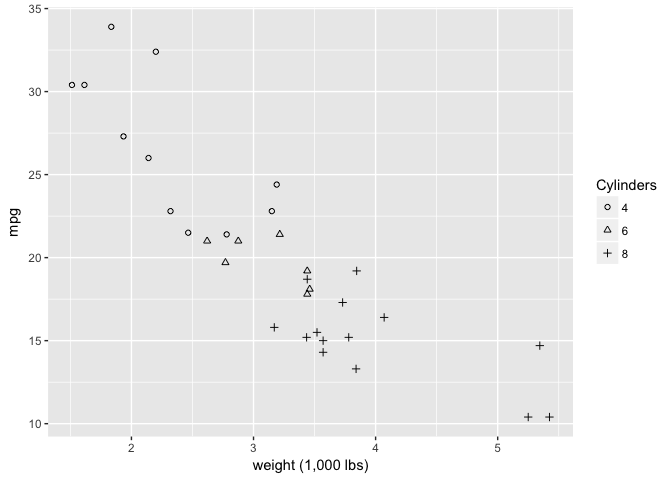
preso_save("img/wt_mpg_scatter_shape2.png")
It’s perfectly ok to redundantly encode using shape and color.
ggplot(mtcars, aes(wt, mpg)) +
geom_point(aes(shape=cyl, color=cyl)) +
xlab("weight (1,000 lbs)") +
scale_shape_manual("Cylinders", values = c(1,2,3)) +
scale_color_brewer("Cylinders", type="qual", palette=1)
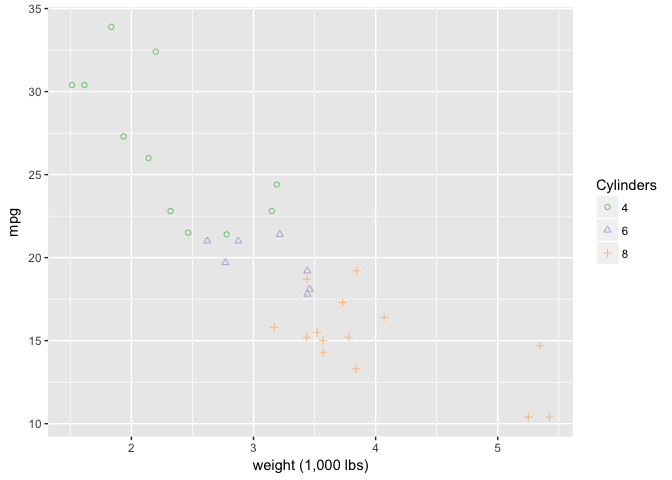
preso_save("img/wt_mpg_scatter_both.png")
You’d think this would be a great encoding, but it’s terrible because of the similar curvature of the sixes and eights.
ggplot(mtcars, aes(wt, mpg)) +
geom_point(aes(shape=cyl), color="black", size=2) +
xlab("weight (1,000 lbs)") +
scale_shape_manual(values = c(52,54,56))
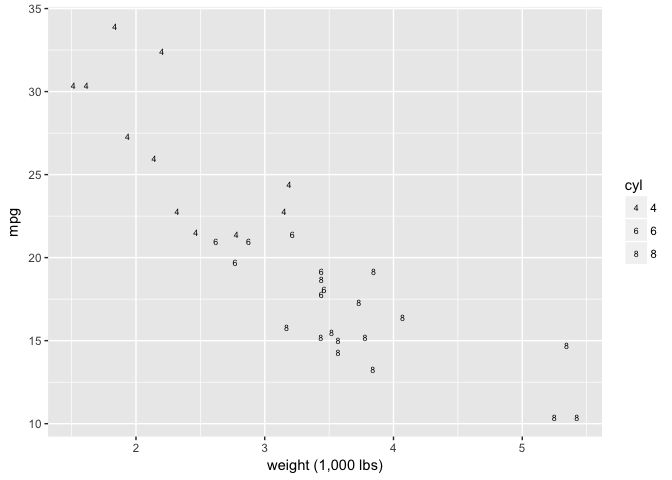
preso_save("img/wt_mpg_scatter_letters.png")
Overlaying linear fits encloses space and makes the grouped objects very strong.
ggplot(mtcars, aes(wt, mpg)) +
geom_point(aes(shape=cyl, color=cyl)) +
geom_smooth(aes(group=cyl, color=cyl), method="lm") +
xlab("weight (1,000 lbs)") +
scale_shape_manual("Cylinders", values = c(1,2,3)) +
scale_color_brewer("Cylinders", type="qual", palette=1)
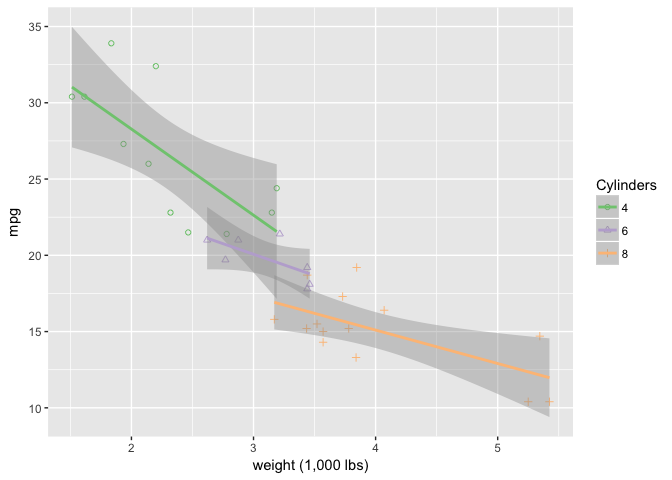
preso_save("img/wt_mpg_scatter_lm.png")
Law of Proximity
A dodged bar chart. Try to compare the blue vs. green bars. I find it very difficult.
ggplot(diamonds, aes(clarity, fill=cut, group=cut)) +
geom_bar(stat="count", position="dodge") +
scale_y_continuous("Count", labels=comma)
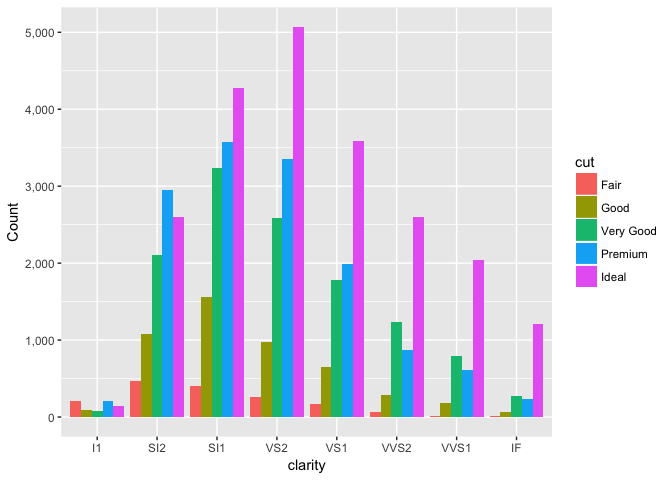
preso_save("img/diamonds_dodge.png")
Assembly with iris data
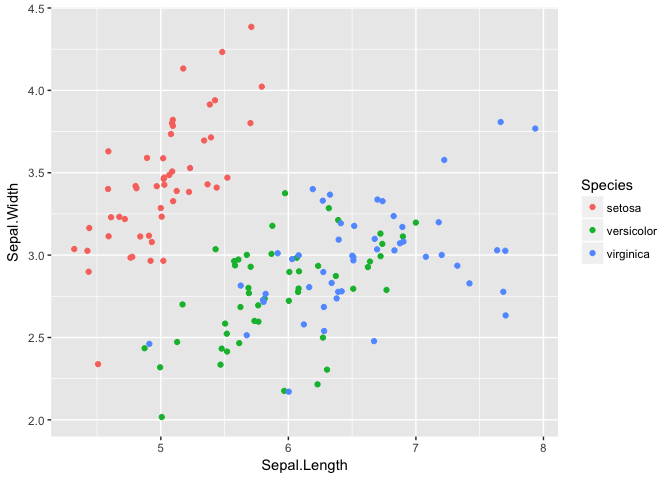
Another dataset that’s good for demonstrating assembly. I didnt use these in the presentation.
ggplot(iris, aes(Sepal.Length, Sepal.Width, color=Species))+geom_jitter()
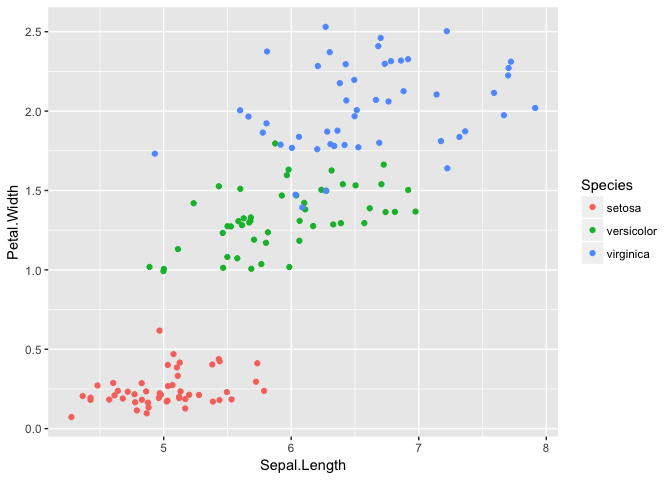
ggplot(iris, aes(Sepal.Length, Petal.Width, color=Species))+geom_jitter()
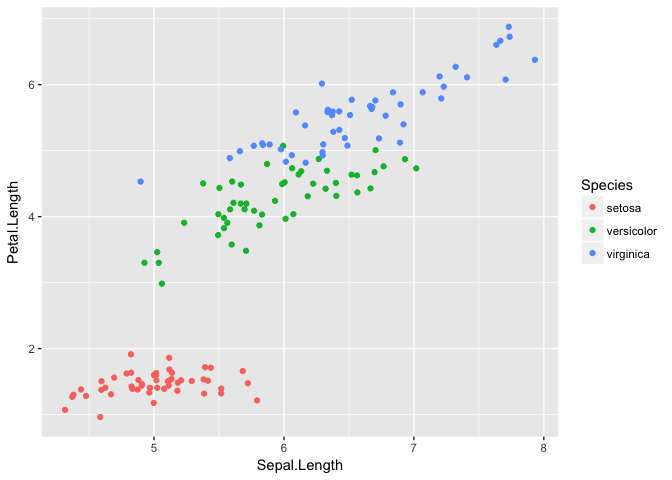
ggplot(iris, aes(Sepal.Length, Petal.Length, color=Species))+geom_jitter()
Part 4: Detection
People frequenty hinder detection by lowering the contrast in luminance.
ggplot(mtcars, aes(wt, mpg)) +
geom_point(color="gray30") +
xlab("weight (1,000 lbs)")
preso_save("img/wt_mpg_scatter_grey.png")
Or by hiding the data with non-data clutter, like gridlines.
ggplot(mtcars, aes(wt, mpg)) +
geom_point(color="black", size=0.2) +
xlab("weight (1,000 lbs)")
preso_save("img/wt_mpg_scatter_small.png")
theme_extras <- theme(panel.grid.major = element_line(colour = "grey20", size = 0.2))
p<-ggplot(mtcars, aes(wt, mpg)) +
geom_point(color="black", size=1.5) +
xlab("weight (1,000 lbs)")
theme_extras <- theme(panel.border = element_rect(fill = NA, colour = "white"),
panel.grid.major = element_line(colour = "white", size = 0.2))
p+theme_extras
preso_save("img/wt_mpg_scatter_grid1.png", theme=theme_preso + theme_extras)
theme_extras <- theme(panel.border = element_rect(fill = NA, colour = "white"),
panel.grid.minor = element_line(colour = "white", size = 0.2),
panel.grid.major = element_line(colour = "white", size = 0.5))
p+theme_extras
preso_save("img/wt_mpg_scatter_grid2.png", theme=theme_preso + theme_extras)
theme_extras <- theme(panel.border = element_rect(fill = NA, colour = "white"),
panel.grid.minor = element_line(colour = "white", size = 0.5),
panel.grid.major = element_line(colour = "white", size = 1))
p+theme_extras
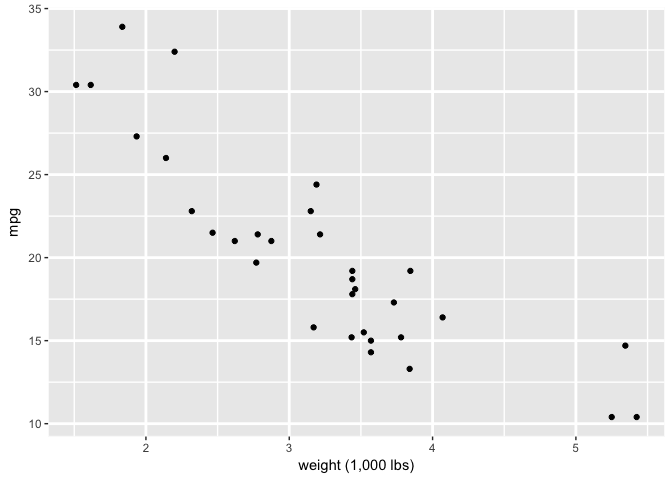
preso_save("img/wt_mpg_scatter_grid4.png", theme=theme_preso + theme_extras)
The Hermann Grid illusion. Do you see the faint grey dots?
theme_extras <- theme(panel.border = element_rect(fill = NA, colour = "white"),
panel.grid.major = element_line(colour = "white", size = 3.5))
ggplot(mtcars, aes(wt, mpg)) +
geom_point(color="black", size=0, alpha=0) +
xlab("weight (1,000 lbs)") + theme_extras
preso_save("img/wt_mpg_scatter_grid3.png", theme=theme_preso + theme_extras)
Decent grid and borders
theme_extras <- theme(panel.border = element_rect(fill = NA, colour = "grey70"),
panel.grid.major = element_line(colour = "grey70", size = 0.2))
p+theme_extras
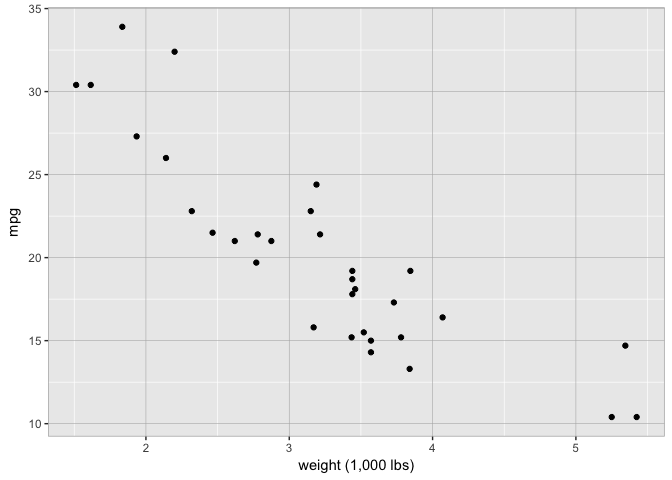
preso_save("img/wt_mpg_scatter_grid5.png", theme=theme_preso + theme_extras)
Part 5: Other Useful results
Weber’s Law
weber <- data.frame(bar = c("c", "a", "b", "bb"),
zpad = c(3, 0, 0, 0),
ylen = c(10, 10.5, 0, 0),
xtop = c(2, 1.5, 0, 0))
weber1 <- weber %>%
select(-xtop) %>%
gather(var, val, -bar)
theme_extras <- theme(axis.title=element_blank(),
axis.text=element_blank(),
axis.ticks=element_blank(),
legend.position="none")
It’s hard to tell if the bars are the same legnth or different.
ggplot(weber1, aes(bar, val, fill=var)) + geom_bar(stat="identity") +
scale_fill_manual(values=c("white", "black")) +
expand_limits(y=c(0,15)) + theme_extras
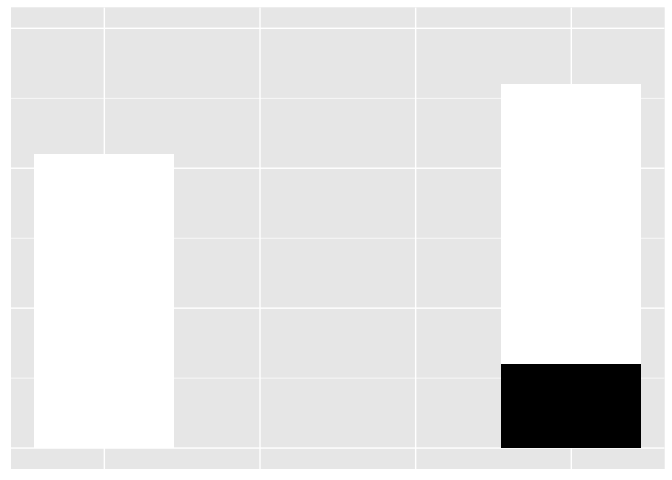
preso_save("img/weber1.png", theme=theme_preso+theme_extras)
But with the little blue ones, it’s easy, even though the absolute difference in length is exactly the same as with the white bars (0.5 units).
weber2 <- weber %>%
gather(var, val, -bar)
ggplot(weber2, aes(bar, val, fill=var)) + geom_bar(stat="identity") +
scale_fill_manual(values=c(muted("blue",l=60), "white", "black")) +
expand_limits(y=c(0,15)) + theme_extras
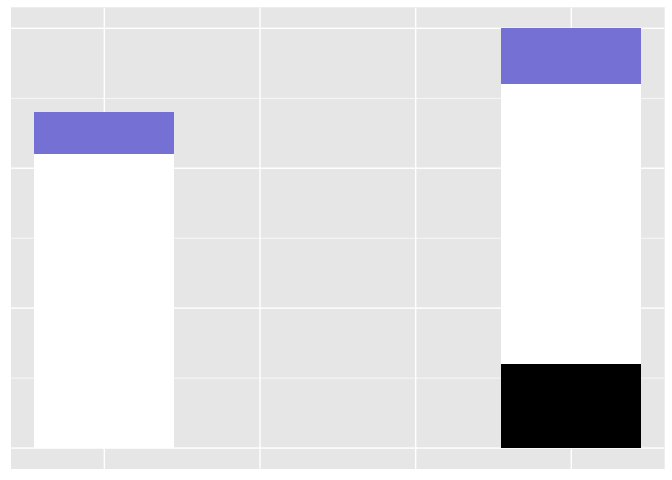
preso_save("img/weber2.png", theme=theme_preso+theme_extras)
Define eight different curves.
to_plot<-data.frame(x=seq(1,100,length.out=500)) %>%
mutate(y=log(x),
y2 = -(((x-100))^2),
y03 = 100-1/x*y,
y04 = 100-2/x*y,
y05 = 100-2/(x+10)*y,
y06 = 100-2/(x+5)*y,
y07 = 99.8-1.5/(x+5)*y,
y08 = 100-2.5/(x+5)*y,
y09 = 100-1.5/(x+52)*y,
y10 = 100-1.5/(x+25)*y
)
Without gridlines it’s hard to compare them precisely.
theme_extras <- theme(axis.title=element_blank(),
axis.text=element_blank(),
axis.ticks=element_blank(),
panel.border = element_rect(fill = NA, colour = "grey70"),
strip.text=element_blank())
ggplot(to_plot %>% select(-y2, -y) %>% gather(var, val, -x),
aes(x,val)) + geom_line(color="black") + facet_wrap(~var, ncol=2) + theme_extras
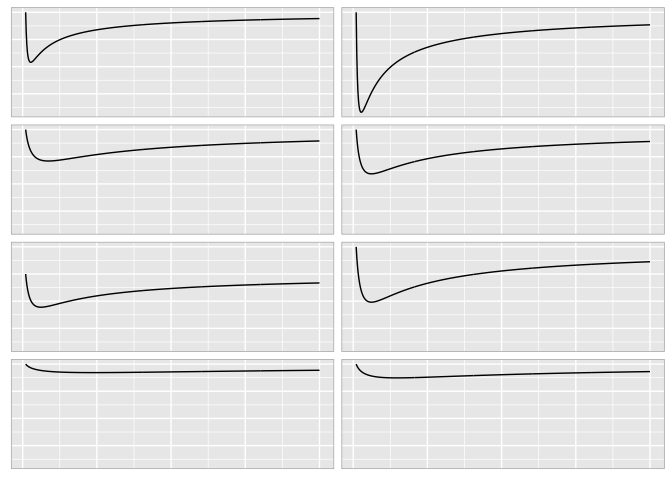
preso_save("img/weber_grid1.png", width=1280/300/2, theme=theme_extras)
It’s much easier with gridlines, because of Weber’s law.
theme_extras <- theme(axis.title=element_blank(),
axis.text=element_blank(),
axis.ticks=element_blank(),
panel.border = element_rect(fill = NA, colour = "grey70"),
panel.grid.major = element_line(colour = "grey60", size = 0.2),
strip.text=element_blank())
ggplot(to_plot %>% select(-y2, -y) %>% gather(var, val, -x),
aes(x,val)) + geom_line(color="black") + facet_wrap(~var, ncol=2) + theme_extras
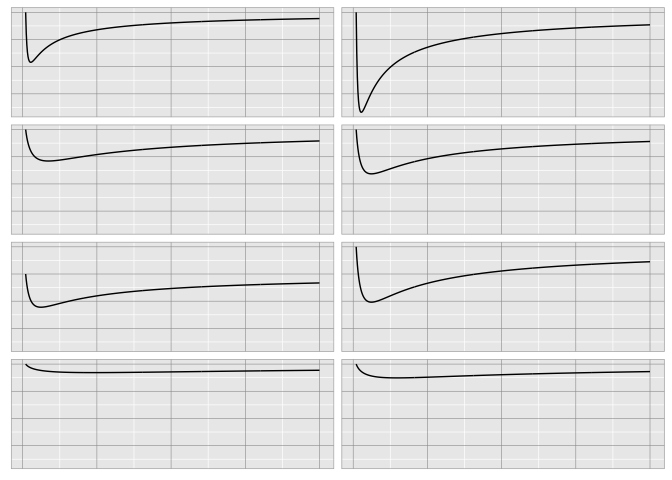
preso_save("img/weber_grid2.png", width=1280/300/2, theme=theme_extras)
You are most sensitive to changes in angle close to 45 degrees
The same data ploteed three ways. It’s easiest to detect the change in slope near 45 degrees.
dat<-data.frame(ct=c(1e6-10000, 1e6, 1e6+15000),
dt=as.Date(c("2016-06-01","2016-06-02", "2016-06-03")))
p<-ggplot(dat, aes(dt, ct)) +
geom_line(group=1, color="black") +
geom_point(color="black") + ylab(NULL) + scale_x_date(NULL, labels=date_format("%b-%d"))
p
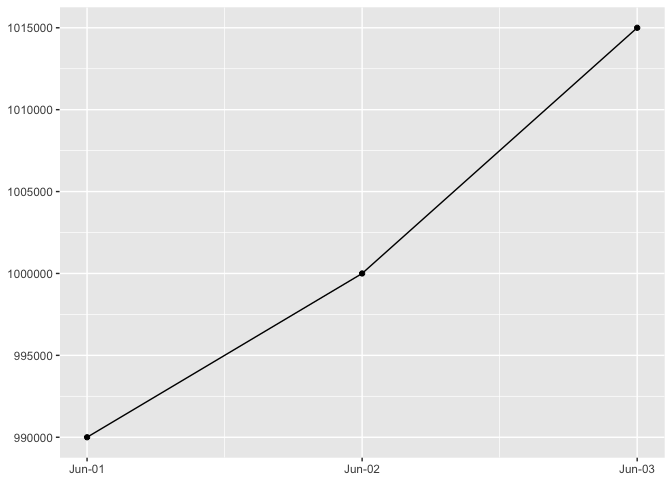
preso_save("img/45deg.png")
p + expand_limits(y=c(800000,1200000))
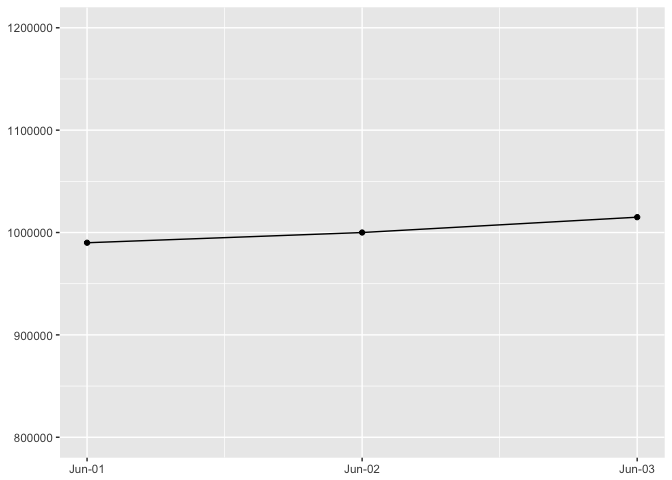
preso_save("img/45deg_tall.png")
p + expand_limits(x=as.Date(c("2016-05-01","2016-07-01")))
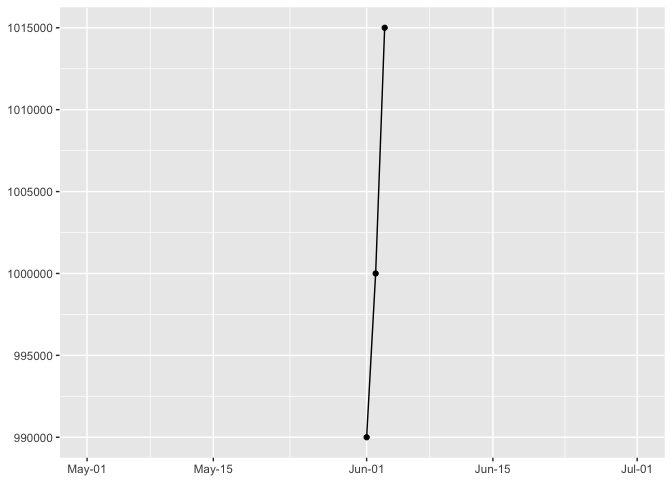
preso_save("img/45deg_wide.png")
Difficult to see with bars (where the y-axis must extend to zero).
ggplot(dat, aes(dt, ct)) +
geom_bar(stat="identity", fill="white") +
ylab(NULL) + scale_x_date(NULL, labels=date_format("%b-%d"))

preso_save("img/45deg_bars.png", width=1280/300/2)
For banking to 45, see the example with the sunspots data in part 6.
The eye measures perdendicular distance
Where is the distance between the lines the greatest?
dat<-data.frame(x=seq(-10, 8, length.out = 100)) %>%
mutate(y=-2*(x^2)+300,
y2=y-seq(30,5,length.out = 100))
dat_w <- dat %>%
gather(var, val, y, y2)
ggplot(dat_w, aes(x, val, group=var))+
geom_line(color="black")
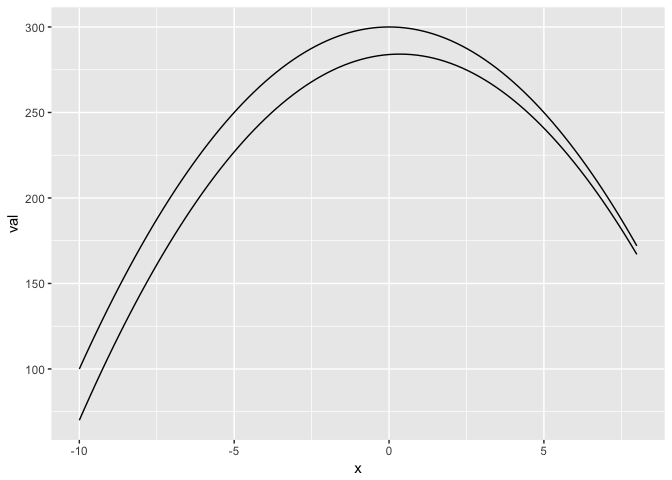
preso_save("img/gap_lines.png", width=1280/300*(2/3))
Here’s the distance plotted directly. Suprisingly, the distance is the largest at the left edge.
ggplot(dat, aes(x, y-y2)) + geom_line(color="black") + ylab("gap")
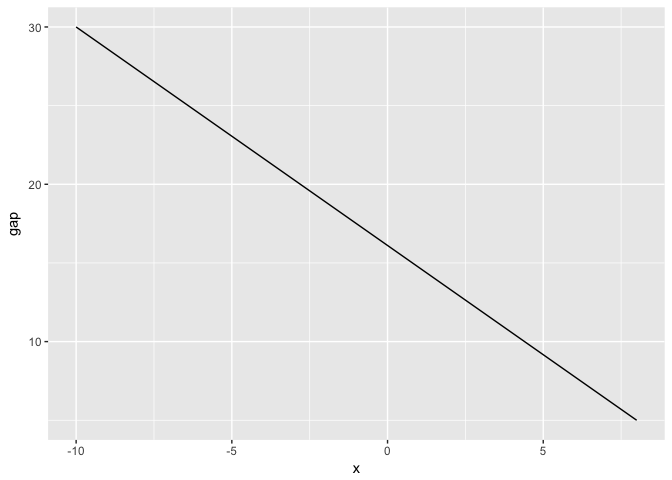
preso_save("img/gap_direct.png")
Y-axis to zero?
See the saturation, area and length examples from the estimation section with mtcars.
With bars the y-axis must go to zero. This obscures the variation in this dataset.
to_plot<-data.frame(x=1:20) %>%
mutate(y=1e6 + 100*x*(-1)^x)
ggplot(to_plot, aes(x,y)) + geom_bar(fill="white",stat="identity") + xlab(NULL) + ylab(NULL)
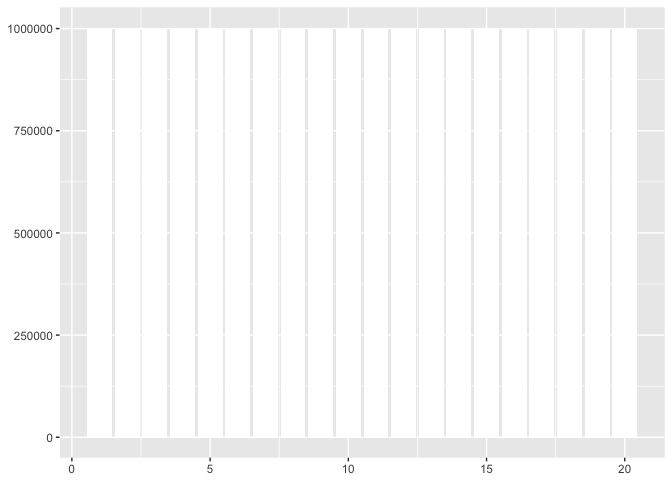
preso_save("img/yaxis_bars.png")
If we switch to points (and position on a common scale), we are free to clip the y-axis to just the relevant interval.
ggplot(to_plot, aes(x,y)) + geom_line(color="black") + geom_point(color="black") + xlab(NULL) + ylab(NULL)
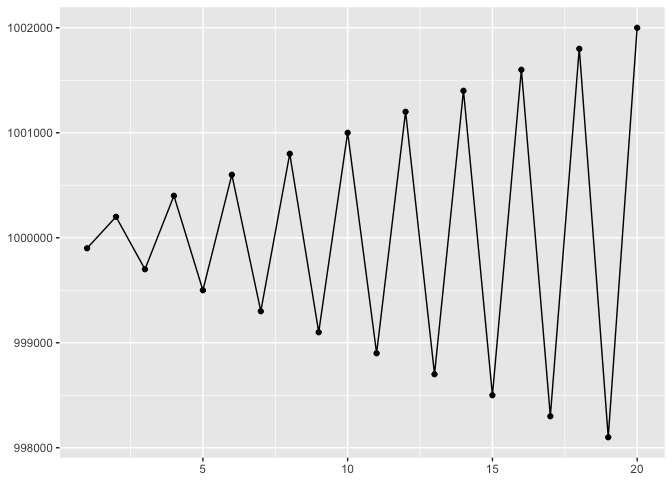
preso_save("img/yaxis_lines.png")
Hue (used carefully) is good for revealing fine structure
ramps<-data.frame(x=seq(-5,5,length.out=200)) %>%
mutate(linear=x/10+0.5,
sigmoid=1/(1+exp(-x)))
theme_extras <- theme(axis.title.y=element_blank(),
axis.text.y=element_blank(),
axis.ticks.y=element_blank(),
legend.position="none")
ggplot(ramps, aes(x,1,fill=sigmoid)) + geom_tile() + theme_extras
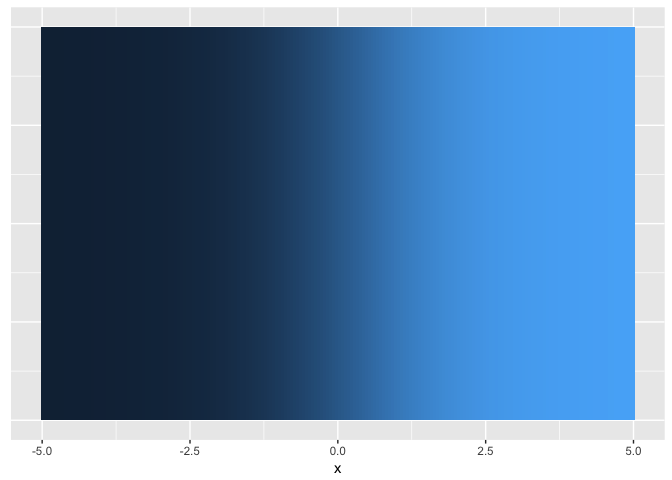
preso_save("img/ramp_sigmoid.png", theme=theme_preso+theme_extras)
ggplot(ramps, aes(x,1,fill=linear)) + geom_tile() + theme_extras
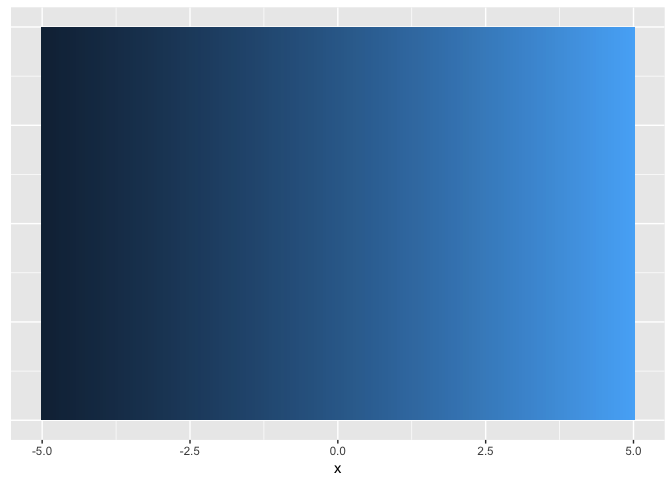
preso_save("img/ramp_linear.png", theme=theme_preso+theme_extras)
theme_extras <- theme(axis.title.y=element_blank(),
axis.text.y=element_blank(),
axis.ticks.y=element_blank())
ggplot(ramps %>% gather(series,value,-x), aes(x,value,color=series)) + geom_line() + theme_extras
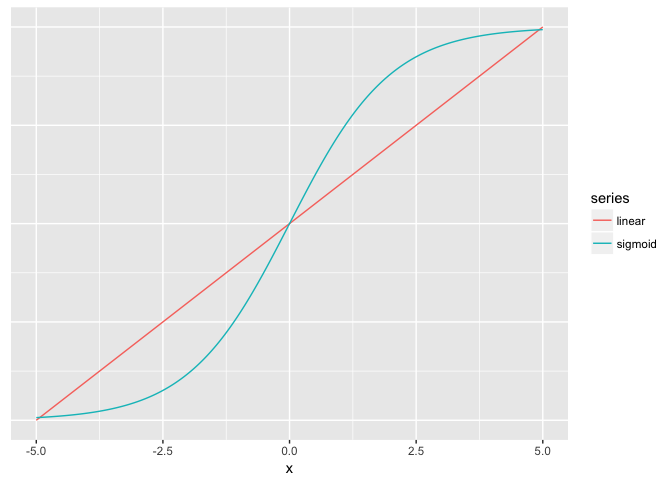
preso_save("img/ramp_both_lines.png", theme=theme_preso+theme_extras)
theme_extras <- theme(axis.title.y=element_blank(),
legend.position="none")
ggplot(ramps %>% gather(series,value,-x), aes(x,series,fill=value)) + geom_tile() + theme_extras
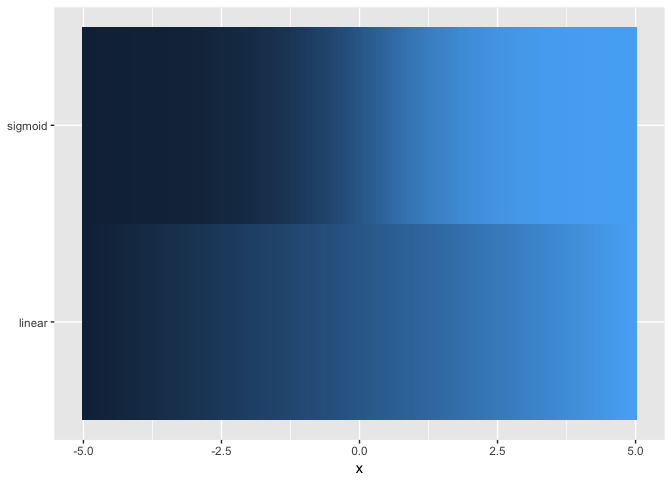
preso_save("img/ramp_both.png", theme=theme_preso+theme_extras)
jet.colors <- colorRampPalette(c("#00007F", "blue", "#007FFF", "cyan", "#7FFF7F", "yellow", "#FF7F00", "red", "#7F0000"))
ggplot(ramps %>% gather(series,value,-x), aes(x,series,fill=value)) + geom_tile() + theme_extras + scale_fill_gradientn(colors = jet.colors(7))
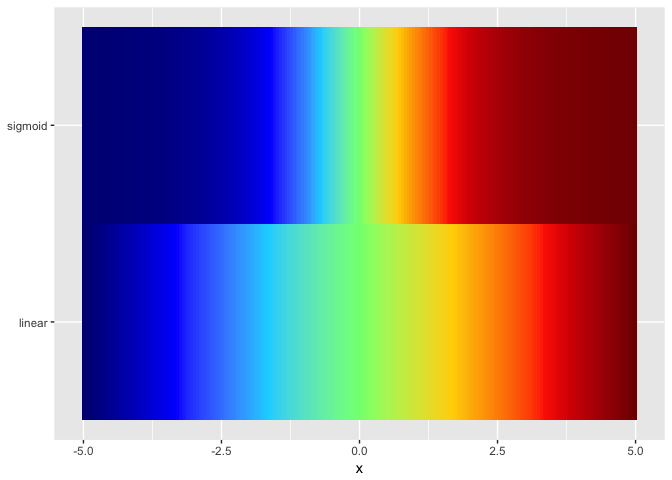
preso_save("img/ramp_both_hue.png", theme=theme_preso+theme_extras)
Viridis not a good as colorjet. Presumably because colorjet traverses more of the space of colors.
ggplot(ramps %>% gather(series,value,-x), aes(x,series,fill=value)) + geom_tile() + theme_extras + scale_fill_viridis()
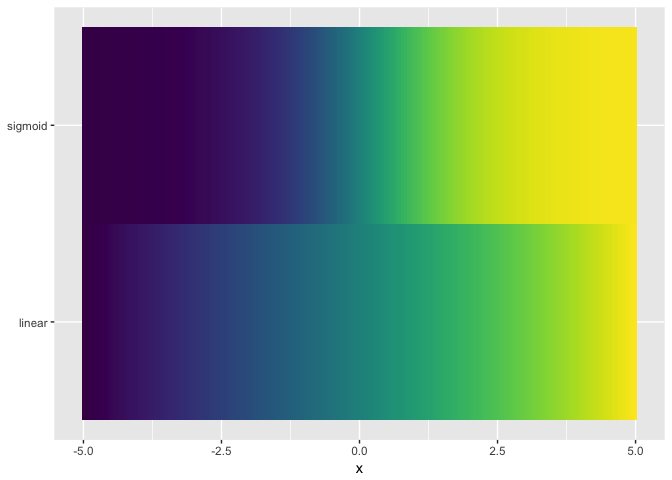
Part 6: Tools/Workflow
Sunspot data
The data is from: http://www.sidc.be/silso/DATA/SN_d_tot_V2.0.txt.
First we load it in and tidy it up.
# Format:
#Line format [character position]:
#- [1-4] Year
#- [6-7] Month
#- [9-10] Day
#- [12-19] Decimal date
#- [22-24] Daily sunspot number
#- [26-30] Standard deviation
#- [33-35] Number of observations
#- [37] Definitive/provisional indicator
positions <- fwf_positions(start=c(1,6,9,12,22,26,33,37),
end=c(4,7,10,19,24,30,35,37),
col_names=c("year", "month", "day", "decimal_date",
"sunspot_number", "std_dev", "n", "provisional"))
sunspots_raw<-read_fwf("http://www.sidc.be/silso/DATA/SN_d_tot_V2.0.txt", col_positions=positions)
## Parsed with column specification:
## cols(
## year = col_integer(),
## month = col_integer(),
## day = col_character(),
## decimal_date = col_double(),
## sunspot_number = col_integer(),
## std_dev = col_double(),
## n = col_integer(),
## provisional = col_character()
## )
sunspots <- sunspots_raw %>%
mutate(day = as.integer(day),
dt = as.Date(sprintf("%4d-%02d-%02d", year, month, day)),
sunspot_number = ifelse(sunspot_number==-1, NA, as.numeric(sunspot_number)),
std_dev = ifelse(std_dev==-1, NA, std_dev),
provisional = !is.na(provisional)) %>%
# There are many missing values before 1850 which complicate analysis
filter(dt >= "1850-01-01") %>%
select(-year, -month, -day, -decimal_date)
summary(sunspots)
## sunspot_number std_dev n provisional
## Min. : 0.00 Min. : 0.000 Min. : 1.000 Mode :logical
## 1st Qu.: 22.00 1st Qu.: 3.600 1st Qu.: 1.000 FALSE:61177
## Median : 65.00 Median : 6.700 Median : 1.000 TRUE :92
## Mean : 84.89 Mean : 7.075 Mean : 4.765
## 3rd Qu.:130.00 3rd Qu.: 9.900 3rd Qu.: 1.000
## Max. :528.00 Max. :77.700 Max. :58.000
## dt
## Min. :1850-01-01
## 1st Qu.:1891-12-09
## Median :1933-11-16
## Mean :1933-11-16
## 3rd Qu.:1975-10-24
## Max. :2017-09-30
A first attempt at plotting… yuck.
ggplot(sunspots, aes(dt, sunspot_number)) +
geom_line(color="black") +
xlab(NULL) + ylab("Sunspot Number")
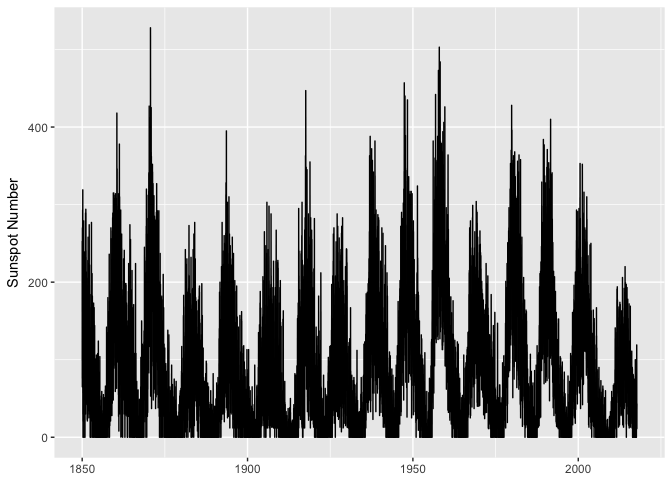
preso_save("img/sunspots_line.png")
Plot as dots, use alpha transparency to reduce overplotting. Notice the gaps between zero and non-zero. You wouldn’t have noticed those without visualization.
ggplot(sunspots, aes(dt, sunspot_number)) +
geom_point(size=0.5, alpha=1/40, color="black") +
xlab(NULL) + ylab("Sunspot Number")
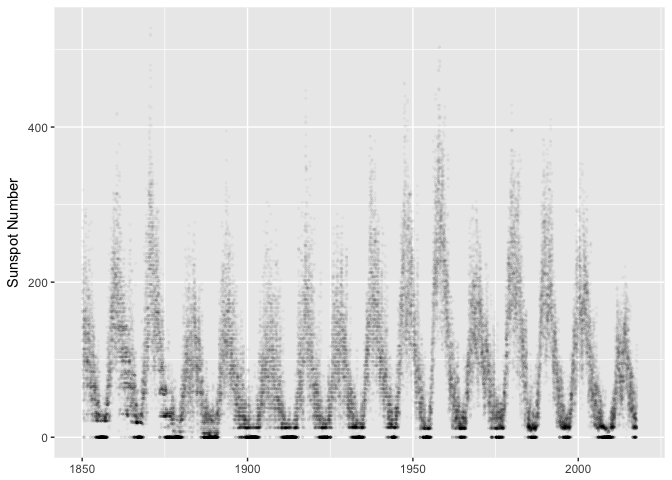
preso_save("img/sunspots_point.png")
There are lots of things we could try to explain about this data, but the most obivous one is the major cycle that’s about 11 years long.
minima <- as.Date("1954-01-01") + seq(-9, 5) * 11 * 365.25
ggplot(sunspots, aes(dt, sunspot_number)) +
geom_point(size=0.5, alpha=1/40, color="black") +
geom_vline(xintercept=as.numeric(minima), color="lightblue") +
xlab(NULL) + ylab("Sunspot Number")
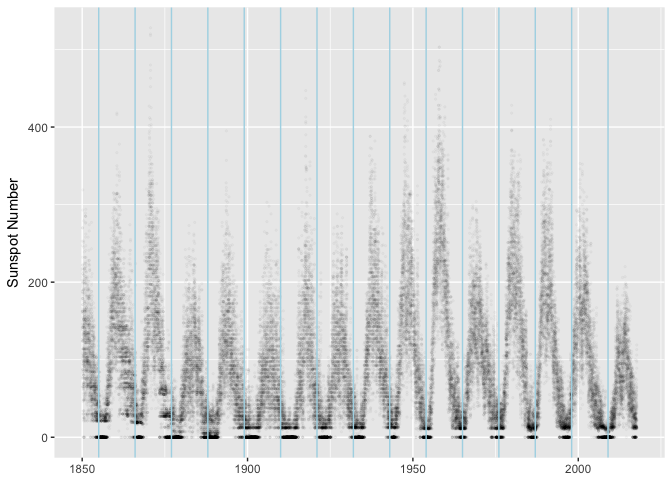
preso_save("img/sunspots_vlines.png")
To make it easier to work with, let’s take monthly averages of the data.
# This works, but it's silly to work on this data at a daily level
#sunspots_ts<- ts(sunspots$sunspot_number, frequency=11*365.25)
#z <- fourier(sunspots_ts, K=3)
#fit <- auto.arima(sunspots_ts, d=1, xreg=z, allowdrift = F, seasonal=FALSE, trace = T)
sunspots_month <- sunspots %>%
mutate(month = as.Date(format(dt, "%Y-%m-01"))) %>%
group_by(month) %>%
summarize(mean_sn = mean(sunspot_number, na.rm=T))
summary(sunspots_month)
## month mean_sn
## Min. :1850-01-01 Min. : 0.00
## 1st Qu.:1891-12-01 1st Qu.: 25.90
## Median :1933-11-01 Median : 72.55
## Mean :1933-10-31 Mean : 84.89
## 3rd Qu.:1975-10-01 3rd Qu.:127.79
## Max. :2017-09-01 Max. :359.39
ggplot(sunspots_month, aes(month, mean_sn)) + geom_line(color="black")
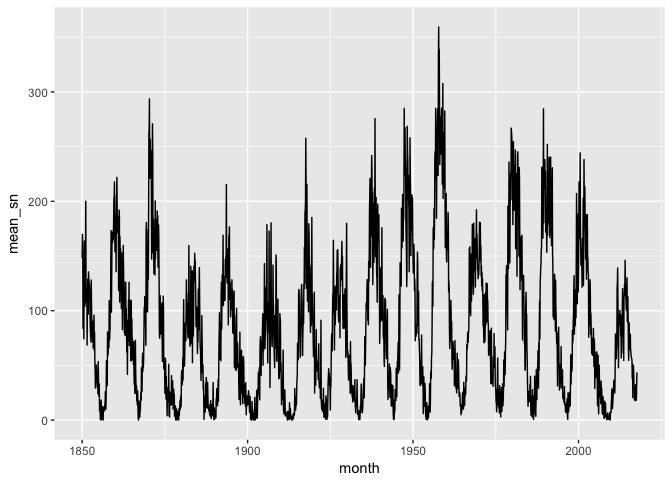
preso_save("img/sunspots_month.png")
#ggplot(sunspots_month, aes(month, mean_sn)) + geom_point(color="black")
Now we can put a loess smoother over the monthly data, and we finally have a nice visualization of the series.
ggplot(sunspots_month, aes(month, mean_sn)) + geom_point(color="black", alpha=1/3) +
geom_smooth(method="loess", span=0.05, n=400) +
xlab(NULL) + ylab("Mean Sunspot Number")
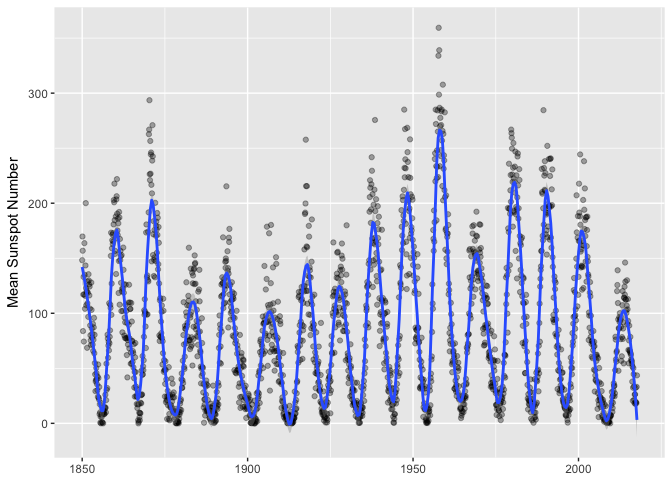
preso_save("img/sunspots_month_smooth.png")
Now let’s impose a model on the data.
library(forecast)
## Warning: package 'forecast' was built under R version 3.4.2
tb<-tbats(sunspots_month$mean_sn,
use.trend=F, use.box.cox=F,
seasonal.periods = c(12*11))
tb_components_mat<-tbats.components(tb)
tb_components<-data.frame(month=sunspots_month$month,
observed = tb_components_mat[,"observed"],
level = tb_components_mat[,"level"],
season = tb_components_mat[,"season"],
residuals = residuals(tb),
fitted = fitted(tb))
tb_components_w <- tb_components %>%
gather(variable, value, -month) %>%
mutate(variable = factor(variable, levels=c("observed", "level", "season", "fitted", "residuals")))
… and visualize the results of the model.
ggplot(tb_components_w %>% filter(variable %in% c("observed","level","season")),
aes(month, value)) +
geom_line(color="black") +
facet_wrap(~variable, ncol=1, scales="free_y")
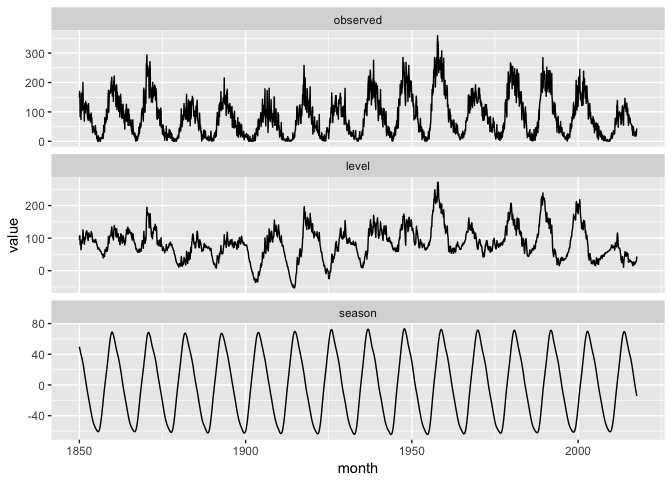
preso_save("img/sunspots_tbats.png")
But is the model good? A common model diagnostic is to look at the “residuals” the difference between the observed data and the model. According to our model, this should be normally distributed with a mean of zero.
binw=5
ggplot(tb_components, aes(residuals)) + geom_histogram(binwidth=binw, fill="lightgrey")
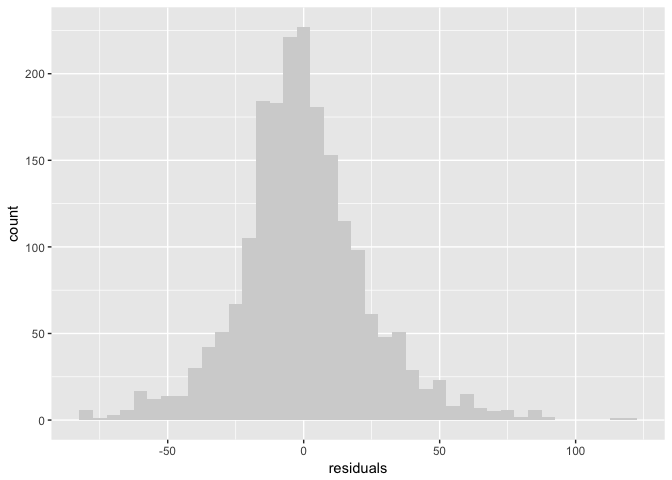
preso_save("img/sunspots_residuals.png")
If you don’t have great intuition about what a normal curve looks like, it can help to overlay one. It look like our model ok, but not great.
curve = data.frame(x=seq(min(tb_components$residuals), max(tb_components$residuals), length.out = 200)) %>%
mutate(y=(binw*length(tb_components$residuals)) * dnorm(x, mean(tb_components$residuals), sd(tb_components$residuals)))
ggplot(tb_components, aes(residuals)) + geom_histogram(binwidth=binw, fill="lightgrey") +
geom_line(data=curve, aes(x,y), color="red")
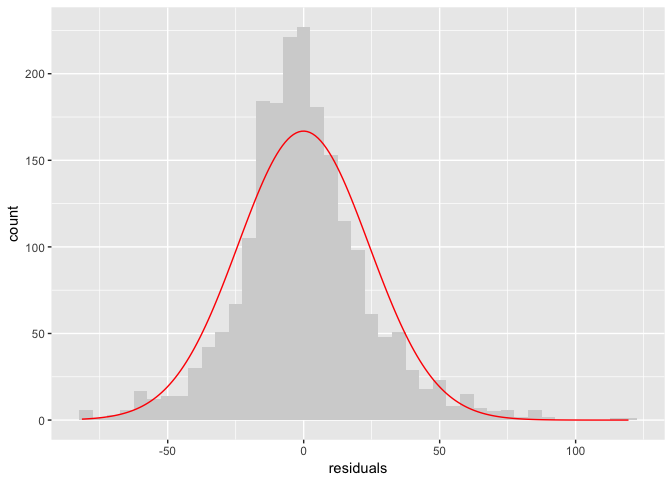
# Other diagnostic plots
qqnorm(residuals(tb))
plot(acf(residuals(tb), lag.max=150))
# 11 year moving average
plot(ma(sunspots$sunspot_number, round(365.25*11)))
Demonstrates banking to 45. There seems to be a pattern of a sharper attack and slower decay.
sunspots_month <- sunspots_month %>%
# mutate(piece = ifelse(month < '1900-01-01', "1850-1900", ifelse(month < '1950-01-01', "1900-1950", "1950-2000"))) %>%
mutate(piece = ifelse(month < '1905-01-01', "1850-1905", ifelse(month < '1960-01-01', "1906-1960", "1960-2015"))) %>%
group_by(piece) %>%
mutate(obs=1:length(month)) %>%
ungroup()
theme_extras <- theme(axis.title.x=element_blank(),
axis.text.x=element_blank(),
axis.ticks.x=element_blank())
ggplot(sunspots_month %>% filter(month < '2015-01-01'),
aes(obs, mean_sn)) + geom_point(color="black", alpha=1/3) +
geom_smooth(method="loess", span=0.05*2, n=150) + facet_wrap(~piece, ncol=1) +
theme_extras +
ylab("Mean Sunspot Number")
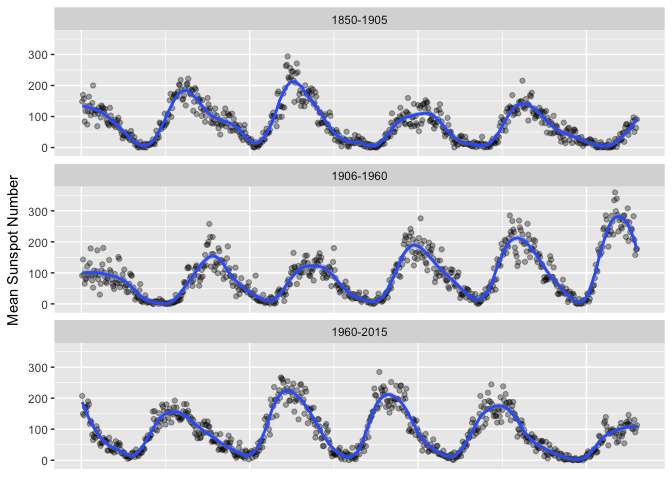
preso_save("img/sunspots_month_wide.png", theme=theme_preso + theme_extras)
Appendix
Barley dataset
library(lattice) # For the barley dataset
# If you want to encourage comparing between years, then put them on a common scale
ggplot(barley, aes(yield, variety, color=year, shape=year))+
geom_point()+facet_wrap(~site)
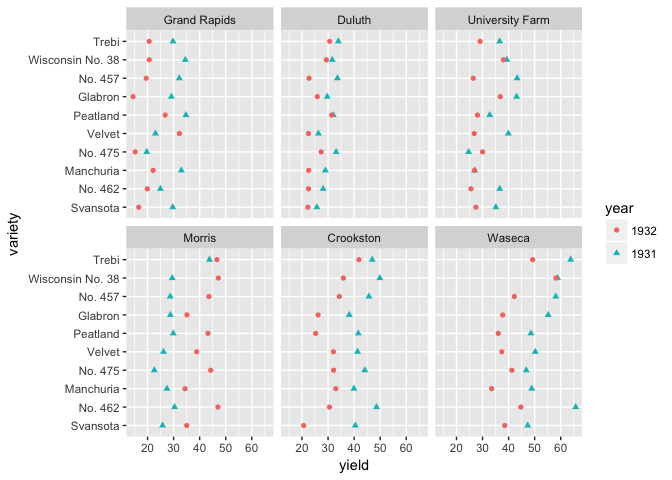
# If you want to encourage comparing between sites, then put them on a common scale
ggplot(barley, aes(variety, yield, group=site, color=site, shape=site))+
geom_point()+geom_line()+facet_wrap(~year)+coord_flip()
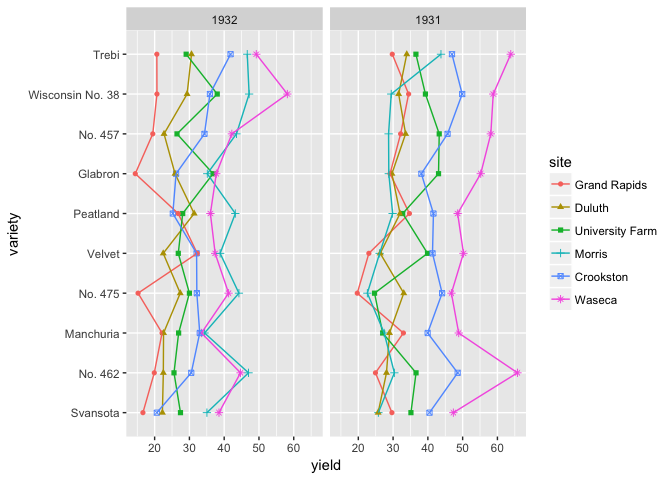
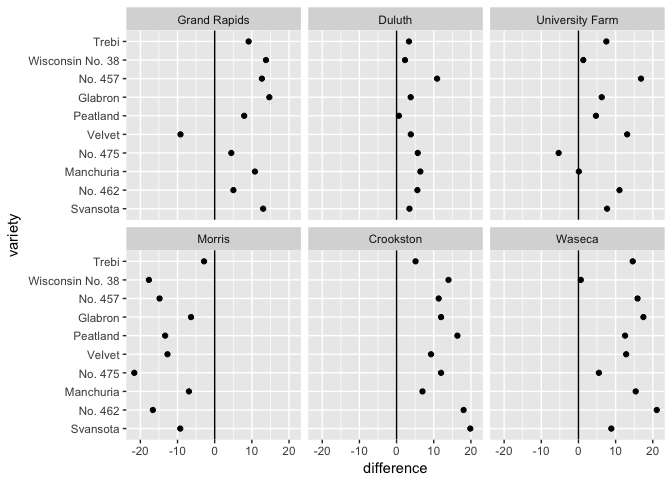
# Can you spot the anomaly?
barley_differences <- barley %>%
group_by(variety, site) %>%
arrange(year) %>%
summarize(difference = yield[2]-yield[1])
ggplot(barley_differences,
aes(difference, variety))+
geom_point(color="black") + facet_wrap(~site)
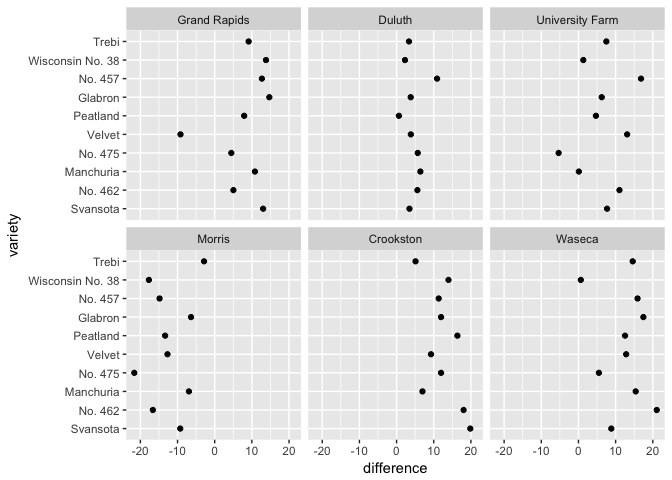
ggplot(barley_differences,
aes(difference, variety))+
geom_point(color="black") + geom_vline(xintercept=0) + facet_wrap(~site)
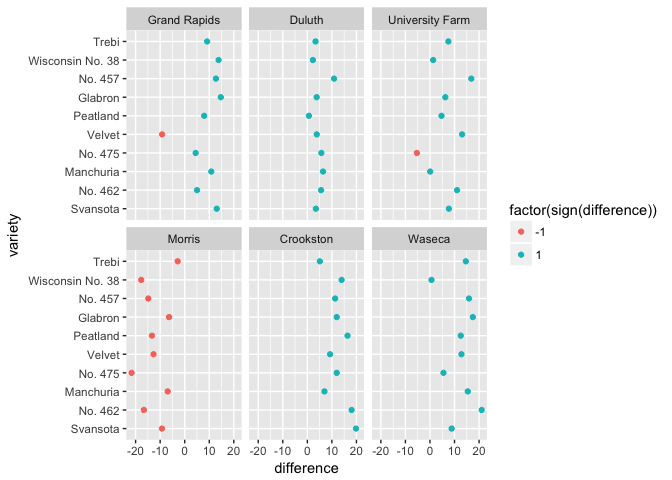
ggplot(barley_differences,
aes(difference, variety, color=factor(sign(difference))))+
geom_point()+facet_wrap(~site)
Session Information
sessionInfo()
## R version 3.4.1 (2017-06-30)
## Platform: x86_64-apple-darwin15.6.0 (64-bit)
## Running under: macOS Sierra 10.12.6
##
## Matrix products: default
## BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
## LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
##
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] lattice_0.20-35 bindrcpp_0.2 gapminder_0.2.0
## [4] viridis_0.4.0 viridisLite_0.2.0 broom_0.4.2
## [7] scales_0.5.0 stringr_1.2.0 tidyr_0.7.1
## [10] dplyr_0.7.4 readr_1.1.1 ggplot2_2.2.1
##
## loaded via a namespace (and not attached):
## [1] Rcpp_0.12.13 RColorBrewer_1.1-2 compiler_3.4.1
## [4] plyr_1.8.4 bindr_0.1 tools_3.4.1
## [7] digest_0.6.12 evaluate_0.10.1 tibble_1.3.4
## [10] gtable_0.2.0 nlme_3.1-131 pkgconfig_2.0.1
## [13] rlang_0.1.2 psych_1.7.8 curl_2.8.1
## [16] yaml_2.1.14 parallel_3.4.1 gridExtra_2.3
## [19] knitr_1.17 hms_0.3 tidyselect_0.2.0
## [22] rprojroot_1.2 grid_3.4.1 glue_1.1.1
## [25] R6_2.2.2 foreign_0.8-69 rmarkdown_1.6
## [28] reshape2_1.4.2 purrr_0.2.3 magrittr_1.5
## [31] backports_1.1.1 htmltools_0.3.6 assertthat_0.2.0
## [34] mnormt_1.5-5 colorspace_1.3-2 labeling_0.3
## [37] stringi_1.1.5 lazyeval_0.2.0 munsell_0.4.3
